Učenje bipedalnog robota da hoda

Autori

Anja Vujanac, učenik IV razreda Gimnazije u Raški.

Tatjana Imbrišić, učenica IV razreda Gimnazije u

Mentori

Nataša Jovanović, diplomirani inženjer elektrotehnike i računarstva, PFE

Dimitrije Pešić, Elektrotehnički fakultet u Beogradu

Slika 1. Grafički apstrakt učenja agenta da hoda pomoću učenja pokrepljivanjem

Apstrakt

Gymnasium okruženje BipedalWalker-v3 je korišćen za upoređivanje tri algoritma: Q-Learning, Twin Delayed Deep Deterministic Policy Gradient (TD3) i Soft Actor-Critic (SAC). Zbog kontinualne prirode problema, Q-Learning se pokazao kao neadekvatan. TD3 je postigao najbolje rezultate zahvaljujući svojoj sposobnosti rada sa kontinualnim problemima. Implementacija SAC algoritma u ovom radu nije uspela da ostvari očekivane performanse. TD3 se pokazao kao najpogodniji algoritam za rešavanje ovog problema, ali su na težem terenu zabeležene nestabilnosti u njegovom ponašanju.

Abstract

The Gymnasium environment BipedalWalker-v3 was used to compare three algorithms: Q-Learning, Twin Delayed Deep Deterministic Policy Gradient (TD3), and Soft Actor-Critic (SAC). Due to the continuous nature of the problem, Q-Learning proved to be inadequate. TD3 achieved the best results thanks to its ability to work with continuous actions. The implementation of the SAC algorithm in this study failed to achieve the expected performance. TD3 proved to be the most suitable algorithm for solving this problem, although instability in its behavior was observed on more challenging terrain.

1. Uvod

Algoritmi za učenje potkrepljivanjem (Reinforcement Learning - RL) predstavljaju pristup mašinskom učenju koji je posebno efikasan u situacijama gde je potrebno učiti kroz interakciju sa okruženjem i optimizovati ponašanje na osnovu posledica donetih odluka. Jedna od važnih primena RL algoritama jeste kontrola kretanja robota, uključujući zadatke poput učenja hodanja kod bipedalnih robota. U ovakvim problemima, agent mora da uči kako da održi ravnotežu, kreće se efikasno i reaguje na različite uslove okruženja - što su izazovi koji zahtevaju sposobnost donošenja kompleksnih odluka u kontinualnom prostoru stanja i akcija.

U prošlosti¹ su korišćeni različiti algoritmi učenja potkrepljenjem za rešavanje zadataka hodanja, uključujući kako klasične metode zasnovane na tabelama (poput Q-Learning alogitma), tako i naprednije metode dubokog učenja koje koriste neuronske mreže za aproksimaciju politika i vrednosti (poput TD3 i SAC). Ovi napredni algoritmi su se pokazali uspešnijim u problemima sa velikim ili kontinualnim prostorom akcija, ali se njihova primena i dalje suočava sa izazovima kao što su stabilnost učenja i generalizacija.

Cilj ovog projekta je da se uporede performanse tri algoritma za učenje potkrepljenjem u Gymnasium okruženju BipedalWalker-v3: Q-Learning, Twin Delayed Deep Deterministic Policy Gradient (TD3) i Soft Actor-Critic (SAC). Hipoteza je da će algoritmi koji su dizajnirani za kontinualne probleme (TD3 i SAC) pokazati značajno bolje performanse u odnosu na diskretan Q-Learning, i da će se među njima moći prepoznati algoritam koji je bolji za ovaj tip problema.

2. Aparatura i metoda

2.1. Okruženje i biblioteke

Svi algoritmi su testirani u okruženju BipedalWalker-v3 koji se nalazi u Gymnasium biblioteci u Python-u. Okruženje sadrži bipedalnog robota koji se sastoji od: trupa sa 2 noge koje imaju po 2 zgloba. Takođe, postoje dva terena u okviru okruženja, a to su: normalan koji je pomalo neravan, i težak koji sadrži stepenice, rupe i prepreke. Da bi teren bio pređen potrebno je da robot skupi određen broj bodova za određen broj vremenskih koraka. Normalan teren traži 300 bodova u 1600 vremenskih koraka, dok u teškom treba da skupi 300 bodova u 2000 vremenskih koraka. Akcija je definisana kao četiri vrednosti veličine u intervalu od -1 do 1, za sva četiri zgloba koji definišu brzinu okretanja motora. Dok se stanje (action, observation) (slika 2.) sastoji od vrednosti za brzinu pomeranja ugla trupa (wh), ugaonu brzinu (θh), horizontalnu brzinu (vh(x)), vertikalnu brzinu (vh(z)), poziciju zglobova i ugaonu brzinu zglobova (w1, w2, w3, w4, θ1, θ2, θ3, θ4), podatka o dodirivanju tla nogama (contact-1, contact-2), kao i vrednosti od 10 Lidar senzora. U vektoru stanja se ne nalaze koordinate.

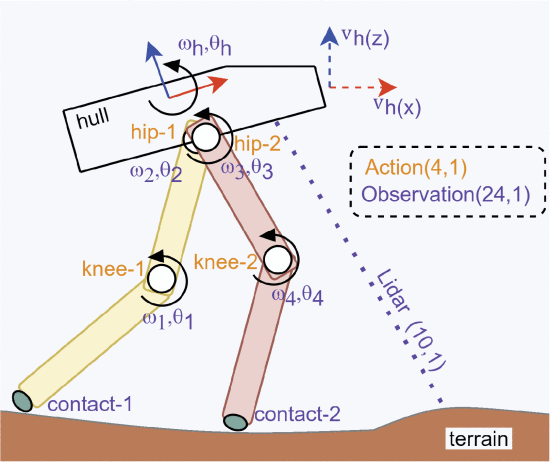Slika 2. Vizuelizacija vektora stanja ¹

Nagrade u samom okruženju se dobijaju za kretanje napred i može da nakupi preko 300 bodova ako stigne do kraja. Ako robotov trup padne na tlo, dobiće -100 bodova (promenjeno na -10 samo radi treniranja na hardcore terenu) i kada koristi zglobove oduzima mu se -0.028 bodova po motoru kojih ima ukupno četiri i nalaze se na zglobovima. U izradi ovog projekta dodate su i nagrade ako robot održava glavu horizontalnom i uspravan oblik tela, kao i nagrade za brzinu kretanja robota, pored one koju dobija iz samog okruženja za pređenu distancu. Takođe su mu dati i negativni bodovi ako dođe do trenutka kada su mu noge „raširene” u kojoj robot izbegava i kretanje i padanje, vrednost uglova oba kuka je zaključeno da bude manja od 0.26 radijana za taj položaj i tada dobija kaznu od -0.03.

U početku simulacije robot se nalazi na krajnjoj levoj strani sa horizontalnim trupom i blago savijenom pozicijom zglobova, odnosno +0.05 radijana na jednom i -0.05 radijana na drugom kolenu. Simulacija će biti završena u slučaju da trup dodatkne pod ili ako robot dođe do desnog kraja terena.

Za beleženje rezultata tokom treniranja i pravljenje grafikona korišćena je bibliotka za Weights and Biases, a za pravljenje neuronskih mreža korišćena je PyTorch biblioteka.

2.2. Q-Learning

Prvi algoritam koji je implementiran je Q-Learning ². Ovaj algoritam pravi Q-tabelu u kojoj čuva svaki par stanja i akcija, i procenjuje korisnost određene akcije u određenom stanju. Q-Learning u svakom koraku posmatra stanje i bira akciju koristeći „ε” (epsilon), odnosno greedy policy. Na početku učenja promenljiva epsilon ima najveću vrednost(250), i ta vrednost predstavlja verovatnoću da će model da uradi nasumičnu radnju. Epsilon se računa na početku svake epizode i jednak je: $$\varepsilon = 1 \div (i \cdot 0.004)$$ jednačina za računanje epsilon vrednosti, gde predstavlja broj trenutne epizode

Takođe ima i 1-ε verovatnoću da će izabrati akciju sa najvećom Q-vrednošću iz tabele. Što više model uči, epsilon vrednost se smanjuje, jer mu je na početku bitno da istražuje, dok je kasnije bitnije da radi očekivane akcije. Nakon urađenog koraka dobija i nagradu iz okruženja, posle čega prelazi u sledeće stanje i koristi Belmanovu jednačinu² da izračuna Q-vrednost prethodnog para stanja i akcije.

$$Q(s,a) = R(s,a) + \gamma*maxa​Q(s′,a)$$

Belmanova jednačina računa Q-vrednost tako što sabira trenutnu nagradu urađene akcije i maksimalnu buduću nagradu pomnoženom sa discount factor-om(γ=0.99) koji predstavlja broj između 1 i 0 pomoću kojeg model odlučuje koliko su trenutne nagrade bitnije od budućih.

2.3. Twin Delayed Deep Deterministic Algorithm (TD3)

TD3 algoritam spada u grupu metoda učenja potkrepljivanjem sa determinističkom politikom (za svako stanje agent vraća jednu akciju), koje se koriste za rešavanje problema sa kontinuiranim prostorom akcija ¹. Osnovna ideja algoritma je da unapredi stabilnost učenja i smanji precenjivanje Q-vrednosti, što su česti problemi u ovakvim zadacima. Da bi to postigao, TD3 uvodi nekoliko ključnih mehanizama: dvostruke kritičke mreže (Double Critics), uglađivanje target politike (Target Policy Smoothing), odsečen dvostruki Q-Learning (Clipped Double Q-Learning) i odlaganje nadogradnje politike (Delayed Policy Updates) ³.

TD3 algoritam se sastoji iz sledećih mreža: jedna akter mreža (generiše akcije na osnovu trenutnog stanja aktera), dve mreže kritičara (procenjuje Q-vrednost akcija koje predlaže akter), i jedna target akter mreža i dve target mreže kritičara (sporije ažurirane kopije odgovarajućih mreža, sa svrhom stabilizacije procesa učenja)

Akter mreža i njena target mreža imaju istu arhitekturu. Imaju ulazni sloj, kroz koji ulaze vrednosti za stanje, on je veličine 24, pošto je stanje vektor dimenzija 24. Ulazne vrednosti na početku prolaze kroz prvi potpuno povezani linearni sloj, sa 400 neurona, čiji izlazne vrednosti prolaze kroz Re-Lu(Rectified Linear Unit)⁴ aktivacionu funkciju koja dodaje nelinearnost i omogućava mreži da nauči složene odnose između stanja i akcija. Nakon njega sledi drugi potpuno povezani linearni sloj, sa 300 neurona, koji takođe implementira Re-Lu aktivacionu funkciju. Izlazni sloj ima četiri neurona koji daju vrednosti akcija koje odgovaraju svakom zglobu u zavisnosti od stanja sa ulaza. Za optimizator, obe mreže koriste Adam optimizator⁵ koji ima stopu učenja(α) od 0.001.

Arhitektura obe mreže kritičara kao i njihovih odgovarajućih target mreža izgledaju isto, a od akter i target akter mreže se razlikuju samo po ulazu i izlazu iz mreže. Ulazni sloj je veličine 28, 24 za komponente stanja, a 4 za akciju odrađenu iz tog stanja. Sledeća dva potpuno povezana linearna sloja su ista kao i kod akter i target akter mreže, prvi ima 400 neurona i koristi Re-Lu aktivacionu funkciju, kao i drugi koji ima 300 neurona. Izlazni sloj kod mreže kritičara i target kritičara ima 1 neuron koji prikazuje pretpostavljenu Q-vrednost za unetu kombinaciju stanja i akcije. Optimizator ovih mreža je takođe Adam optimizator sa stopom učenja(β) od 0.001.

Target Policy Smoothing predstavlja mehanizam koji pri izračunavanju target Q-vrednosti od target kritičara dodaje šum akcijama target aktera. Čime smanjuje precenjivanje Q-vrednosti, što ultimativno čini učenje stabilnijim i otpornijim na male promene i greške.

Clipped Double Q-Learning je još jedan način smanjivanja rizika precenjivanja pri čemu mreže kritičara istvoremeno računaju Q-vrednost, ali za konačnu vrednost se bira manja pretpostavka. Pošto je bolje da agent potcenjuje Q-vrednosti nego da ih preceni. U slučaju da agent preceni efikasnost određenih akcija, postoji velika šansa da će se zaglaviti radeći samo te akcije, bez da istraži ostale slučajeve koji bi mogli biti bolji od onoga što je do sad radio.

Delayed Policy Updates je mehanizam gde se akter mreža ažurira ređe (na svaki drugi korak), dok se kritičari ažuriraju na svakom koraku. Ovim se održava stabilnost učenja i smanjuje učestalost menjanja politike.

Na svakom koraku tokom učenja agent izvršava akciju koju je predložio akter i dobija odgovarajuću nagradu iz okruženja. Izvršen korak (njegovo stanje, akcija, dobijena nagrada, kao i sledeće stanje) se potom čuva u memoriji (Replay Buffer) gde može da se sačuva i do milion trenutaka, odakle se nasumično uzimaju male količine podataka (100 instanci) za treniranje mreža na svakom sledećem koraku. Replay buffer se koristi da ne bi postojala korelacija izmedju uzastopnih stanja pri učenju. Mreže kritičara se ažuriraju na osnovu target Q-vrednosti dobijene pomoću target mreža. Akter se ažurira na svaka dva koraka tako što koristi gradijent koji potiče iz kritičara i optimizuje svoje akcije tako da maksimizuje predpostavljenu Q-vrednost. Target mreže se ažuriraju metodom „sporog prepisivanja” (Soft Updates) što znači da na svakom koraku target mreže polako pomeraju svoje vrednosti ka onima u glavnim mrežama tako što pomnože trenutnu vrednost obične mreže sa veoma malim brojem tau (τ=0.005) i saberu ga sa proizvodom trenutne vrednosti target mreže sa 1-τ.

Funkcija pomoću koje se updejtuju target mreže: $$\theta’_{i}=\tau\cdot \theta_{i}+(1-\tau)\cdot\theta’_{i}$$

2.3. Soft Actor Critic (SAC)

Soft Actor Critic je stohastični akter-kritičar algoritam koji je napravljen za kontinualne probleme sa skoro beskonačnim mogućim brojem stanja i akcija[6]. Stohastični algoritam vraća parametre Gausove raspodele (srednju vrednost i standardnu devijaciju) iz koje se nasumično izvršava akcija, za razliku od TD3 algoritma, koji bira jednu da vrati samo jednu akciju koja će se izvršiti.

Stohastična politika SAC algoritma se sastoji iz sledećih mreža: stohastičkog aktera, dva kritičara i dva target kritičara.

Akter mreža u SAC algoritmu dosta liči na akter mrežu TD3 algoritma, ulaz prima 24 konstanti koje predstavljaju stanje, ima 2 skrivena potpuno povezana linearna sloja koja implementiraju Re-Lu aktivacionu funkciju. Mreža takođe koristi Adam optimizator ali sa stopom učenja(α) od 0.0004. Još jedna od razlika je veličina 2 skrivena sloja, dok je u TD3 prvi skriveni sloj 400, a drugi 300, u Soft Actor Critic algoritmu su prvi i drugi skriveni sloj veličine 256, takođe se razlikuje i izlaz iz mreže. Pošto je TD3 deterministički algoritam on ima jedan izlaz(vektor sa 4 dimenzije), dok je SAC stohastični algoritam koji ima 2 paralelna izlaza, prvi izlaz je srednja vrednost akcije, a drugi je standardna devijacija te vrednosti. To znači da agent uz pomoć ta 2 izlaza može da izvuče Gausovu raspodelu odakle će izabrati jednu akciju, što je i osnovna karakteristika stohastičnosti i omogućava izvršavanje različitih akcija za isti izlaz iz mreže.

Mreža dva kritičara i dva target kritičara SAC algoritma je takođe veoma slična prethodnim mrežama. Na ulazu dolazi 28 vrednosti, 24 za stanje i 4 za vektor akcije. Ima 2 potpuno povezana linearna sloja koja implementiraju Re-Lu aktivacionu funkciju, oba sloja veličine 256, Izlazni sloj ima samo 1 neuron koji vraća pretpostavljenu Q-vrednost. Koristi Adam optimizator sa stopom učenja(β) od 0.0004. SAC takodje implementira Clipped Double Q-Learning kod svojih kritičara.

Glavna osobina SAC algoritma je njegova implementacija entropije u target funkciji i merenje koliko se nasumično ponaša agent. Target funkcija⁶: $$J(\pi)=\sum_{t=o}^{T} E_{(s_t,a_{t})\sim p_{\pi}}[r(s_t,a_t)+\alpha H(\pi(\cdot |s_t))]$$

Algoritam pokušava da maksimizuje ovu funkciju dok trenira agenta da bi postojao balans izmedju maksimizacije nagrade i zadržavanju nasumičnosti.

π- politika (akter)

$s_t, a_t$- stanje i akcija u koraku u vremenu t

$p_{\pi}$- distribucija stanja i akcija dobijena ako agent prati politiku

$r(s_t,a_t)$- nagrada koju agent dobija ako iz stanja izvrši akciju

$H(\pi(\cdot |s_t))$- entropija politike u stanju (meri koliko je akcija „nasumična”)

$\alpha$- koeficijent koji balansira maksimizaciju nagrade i entropije

Sva iskustva (stanje, akcija, nagrada, sledeće stanje) se kao i u TD3 algoritmu čuvaju u Replay Buffer-u (memorija koja čuva do milion koraka) da bi se mreže trenirale na nasumično odabranim grupama(skupina od 256 instanci) iskustva. Tako algoritmi smanjuju povezanost kod uzastopnih podataka što čini učenje stabilnijim.

Dve mreže kritičara, kao i u TD3 algoritmu, smanjuju precenjivanje Q-vrednosti biranjem manje predikcije, dok njihove target mreže koriste Soft Update mehanizam.

2.4. TD3 u Hardcore orkuženju

Na Hardcore orkuženju je treniran samo model koji primenjuje TD3 algoritam zbog njegove sposobnosti da se dobro adaptira datom problemu. Da bi se model naučio na hardcore terenu, nagrade koje se dobijaju od okruženja nisu bile dovoljne. Do ovog zaključka je dođeno nakon pokušanog treniranja agenta u nepromenjenom okruženju. Pri čemu je agent izbegavao kretanje jer bi mu kazna za pad (-100 bodova) prouzrokovana istraživanjem, postala mnogo gora od stajanja u mestu. Kazna za pad je smanjena na -10 bodova što je rešilo uočeni problem i ponovo podstaklo istraživanje.

Na teškom terenu BipedalWalker-v3 okruženja treniran je samo TD3 algoritam, jer se u prethodnim eksperimentima pokazao kao najefikasniji. Standardna nagrada okruženja u osnovnoj verziji sadrži veliku kaznu za pad (-100 bodova), što dovodi do toga da agent razvija strategiju izbegavanja kretanja - stajanje u mestu mu donosi više bodova nego da pokuša da hoda što bi potencijalno prouzrokovalo pad. Tokom implementacije TD3 algoritma mogli smo da uočimo zaglavljivanje agenta zbog loše određenih nagrada i kazni. Kada bi počeo da izbegava pokušavanje hodanja, pri čemu bi samo raširio noge, odnosno zauzeo položaj špage ili polušage, čime bi odstranio mogućnost pada na tlo. Do ovoga je došlo zbog isuviše velike kazne za pad koja je sprečila agenta da da prioritet istaživanju. Da bi se podstaklo istraživanje i omogućilo učenje hodanja, kazna za pad je smanjena na -10. Ova modifikacija nagradne funkcije omogućila je agentu da češće istražuje i efikasnije uči u kompleksnijem okruženju.

3.Rezultati

3.1. Q-Learning

Bodovi po epizodama za Q-Learning se može videti na slici 3. Na početku treniranja je varirao između -350 do -100, dok je posle tristote epizode agent osvajao konstantno bodove oko -100 poena. Odatle možemo da uvidimo da Q-learning nije adekvatan za ovaj tip problema. Do toga je došlo jer Q-Learning algoritam nije dizajniran za kontinualne probleme i radi po principu Q-tabele koju popunjava sa svakim mogućim stanjem i akcijom, što je moguće samo kod diskretnih problema koji imaju ograničen broj stanja i akcija. Nasuprot tome, BipedalWalker-v3 je kontinualno okruženje što znači da broj mogućih kombinacija stanja i akcija možemo posmatrati kao beskonačan, te algoritam nije mogao da napreduje u učenju. Tokom treninga agent bi brzo padao na tlo.

Slika 3. Rezultati Q-Learning algoritma u 1000 epizoda

3.2. Twin Delayed Deep Deterministic Algorithm (TD3)

TD3 je na početku treniranja tokom učenja imao oko -100 poena, dok je na 200 epizodi krenuo nagli rast osvojenih bodova i bolji rezultati. Oko 300-350 epizode moguće je primetiti nagli pad u bodovima koji se naziva katastrofalno zaboravljanje koja može da se desi nakon što se replay buffer napuni novim epizodama i zaboravi stare korisne epizode, takođe je moguće da se overfit-ovao (prenaučio) na mali sample dobrih epizoda. Nakon katastrofalnog zaboravljanja agent se brzo uči i dostiže prosek od 300 bodova po epizodi nakon četiristote epizode, mada mogu da se primete pojedine instance gde je agent iskusio iznenadan pad u rezultatima, za čije postojanje je verovatno krivo agentovo istraživanje.

Funkcija gubitka na kratko opada pri početku treniranja, zatim naglo raste i posle toga nastavlja da opada do kraja učenja. Takođe može da se primeti veći pad u gubitku malo pred katastrofalno zaboravljanje, i njegov blagi rast pri agentovom ponovnom učenju i povratku na bolje rezultate.

TD3 je pokazao značajno bolje performanse, pošto je algoritam predviđen za rad na kontinualnim problemima. Tokom treninga agent je postepeno učio da održava ravnotežu i da se efikasno kreće kroz teren, mada je pokazao i blago nestabilne rezultate sa iznenadim padovima u bodovima.

Slika 4. Rezultat TD3 algoritma

Slika 5. Akter funkcija gubitka TD3 algoritma

3.3. Soft Actor Critic (SAC)

Za razliku od rezultata u drugim radovima, SAC nikada nije uspeo da dobije pozitivnu količinu bodova (slika 6.). Mada može da se vidi neznatno povišenje prosečnog rezultata kroz epizode. Sa druge strane, akter funkcija gubitka (slika 7.) postepeno opada, što bi trebalo da predstavlja da je politika formalno učila u skladu sa target funkcijom, ali se to nije pokazalo kroz bolje akcije u okruženju. Mogući uzroci bi mogli biti neprilagođeni hiperparametri u primeni.

Slika 6. Rezultat SAC algoritma

Slika 7. Akter funkcija gubitka SAC algoritma

3.4. Twin Delayed Deep Deterministic Algorithm (TD3) u Hardcore okruženju

Može se primetiti da prosek osvojenih poena na 1700 epizoda za TD3 algoritam na teškom terenu (slika 8.) ima rast, i na određenim epizodama prelazi 200 poena (najviše je osvojeno 241), mada nikada ne dostiže do 300 poena, te samim tim nikada i ne prelazi ceo teren. Osvojeni poeni i u kasnijoj fazi treniranja (posle hiljadite epizode) nisu uvek konstantni i varijaju sa razlikama i do 300 poena između uzastopnih epizoda.

Funkcija gubitka aktera TD3 agenta na teškom terenu (slika 9.) nam pokazuje rast gubitka na početku učenja. Prosečni gubitak kroz epizode se polako stabilizuje, da bi se posle hiljadite epizode video blagi pad i ponovna stabilizacija. Oscilacije nam pokazuju da je agent idalje pokušavao da promeni politiku i da se prilagodi kompleksnom terenu. Te oscilacije se takođe i poklapaju sa nestailnim nagradama tokom treniranja.

TD3 algoritam se u hardcore okruženju pokazao kao nestabilan i nepouzdan. Iako su izmene nagradne funkcije donekle poboljšale agentovo istraživanje, rezultati su i dalje varirali - ponekad agent postiže odlične performanse, dok u većini epizoda brzo pada na tlo. Najverovatniji razlog ove nestabilnosti je i dalje neidealna nagradna funkcija i složenost terena, koja otežava agentu da generalizuje naučenu politiku.

Slika 8. Rezultat TD3 algoritma na teškom terenu

Slika 9. Funkcija akterovog gubitka TD3 algoritma na teškom terenu

4. Zaključak

Tokom ovog projekta istraženo je ponašanje tri algoritma za učenje potkrepljenjem u Gymnasium okruženju BipedalWalker-v3: Q-Learning, TD3 i SAC. TD3 se pokazao kao najefikasniji za predstavljeni problem, jer uspešno uči politiku hodanja i održava ravnotežu u standardnom okruženju, dok Q-Learning nije bio primenljiv zbog ogromnog prostora stanja i akcija. Implementacija SAC algoritma nije uspela da ostvari očekivane rezultate, iako je funkcija gubitka izgledala stabilno, što ukazuje na izazove sa istraživanjem i adaptacijom politike u ovom specifičnom okruženju.

Ovi rezultati dovode do boljeg razumevanja ponašanja naprednih algoritama za učenje potkrepljenjem u zadacima sa kontinualnim problemima i naglašavaju potrebu za daljim istraživanjem hiperparametara, modifikacijom nagradne funkcije i potencijalnog kombinovanja metoda za postizanje stabilnijeg učenja u kompleksnim okruženjima.

6. Reference