Predviđanje rezultata Formule 1

Polaznici: Darija Vasiljević, Marina Stojilković
Mentori: Andrej Bantulić, Milica Gojak i Marija Nedeljković

Apstrakt

U ovom radu razvijen je sistem za predviđanje konačnog redosleda vozača u trkama Formule 1 koristeći javno dostupne podatke iz perioda 2018-2024 godine. Upoređene su performanse statističkih modela (linearna regresija, SVM, Naivni Bajes) i savremenih algoritama mašinskog učenja (duboke neuronske mreže i XGBoost) koji su trenirani nad malim skupom podataka. Razmatrana su dva pristupa: listwise (predviđanje cele liste) i pairwise (predviđanje vozača na boljoj poziciji iz parova). Evaluacija modela pokazuje da pairwise pristupi, naročito XGBoost treniran nad parovima, postižu najbolje performanse: RMSE = 1.58, NDCG = 0.987, MRR = 0.89, Kendall’s $\tau$ = 0.86 i Spearman = 0.92, što ukazuje na precizno rangiranje vozača i visoku tačnost predviđanja pobednika. Rad demonstrira da kombinacija obrade karakteristika i modernih modela može značajno unaprediti predikciju rezultata u dinamičnom sportu poput Formule 1.

Abstract

This paper presents a system for predicting the final standings of drivers in Formula 1 races using publicly available data from 2018 to 2024. The performance of statistical models (linear regression, Support Vector Machine, Naive Bayes) and modern machine learning algorithms (deep neural networks and XGBoost) was compared on a relatively small dataset. Two approaches were considered: listwise (predicting the entire ranking) and pairwise (predicting which driver in a pair will achieve a better position). Model evaluation shows that pairwise approaches, especially XGBoost trained on driver pairs, achieve the best performance: RMSE = 1.58, NDCG = 0.987, MRR = 0.89, Kendall’s $\tau$ = 0.86, and Spearman = 0.92, indicating accurate driver ranking and high precision in predicting race winners. The study demonstrates that combining feature engineering with modern models can significantly improve race outcome predictions in a dynamic sport like Formula 1.

1. Uvod

Formula 1 je sport koji se u velikoj meri oslanja na analizu podataka. Informacije koje timovi prikupljaju u toku trkačkih vikenda su veoma značajne za osmišljanje adekvatne strategije za trku, podešavanje bolida, otkrivanje potencijalnih problema i unapređenje bolida. Za vreme trke i pripremnih treninga prikupljaju se podaci sa preko 250 senzora na bolidu. U toku jednog kruga prikupi se oko 30MB podataka. U Mercedesu tvrde da tokom jednog vikenada prikupe preko jednog terabajta podataka.
Većina prethodnih radova koji se bave predviđanjem rerzultata trke Formule 1 nemaju cilj da rangiraju sve vozače. Na primer, rad [1] bavi se klasifikacijom vozača na kraju trke u 4 klase. Klasa 0 predstavlja pozicije od 11. do 20, klasa 1 od 7. do 10. mesta, klasa 2 uključuje 4, 5. i 6. poziciju, dok klasa 3 obuhvata prva 3 mesta. Ovakav pristup ima tačnost 65% kada se koristi duboka neuralna mreža (DNN) mreža. Umesto dobijanja cele rang-liste, dobija se klasifikacija u 4 klase, što značajno ograničava praktičnu primenu. Model ne može steći adekvatnu sliku o performansama vozača, niti pružiti uvid u mogući tok trke ili se koristiti za kompleksnija predviđanja.
Cilj ovog projekta je konstruisanje sistema koji, koristeći javno dostupne podatke, predviđa poredak vozača na kraju trke.

2.Metod

2.1.Podaci i karakteristike

Podaci o vozačima, stazama, konstruktorima, rezultatima trka, kvalifikacija, sprintova, kao i poredak vozača u svakom krugu trke i njihova vremena su preuzeti sa Jolpica F1 API-ja. Podaci o vremenskim uslovima su dobijeni pomoću Fast F1 biblioteke u Python-u. Inicijalno bilo je predviđeno da se koriste podaci od početka hibridne ere (2014), jer je tada došlo do promene pravila i sama dinamika sporta se dosta promenila. Međutim, podaci o vremenskim uslovima iz Fast F1 biblioteke dostupni su tek od 2018. Stoga, odlučeno je da skup podataka sadrži trke od 2018. do 2024. godine, ukupno 7 sezona. Od korišćenih karakteristika, 18 je direktno preuzeto iz prethodno navedenih izvora dok je 10 izvedeno na osnovu postojećih podataka. Karakteristike koje se koriste u ovom radu prikazane su u tabeli 1.

Grupa	Karakteristike	Objašnjenje
Opšte informacije	sezona, runda, naziv trke, sprint vikend	Osnovne informacije o Velikoj nagradi.
Vozač i tim	broj vozača, identifikator vozača, tim	Identifikacija vozača i tima.
Performanse	kvalifikaciona pozicija, startna pozicija	Rezultati vozača tokom vikenda pre trke.
Staza	naziv staze, dužina kruga, broj krugova, broj krivina	Karakteristike staze.
Vremenski uslovi	temperatura vazduha, vlažnost vazduha, pritisak, temperatura staze, brzina vetra, pravac vetra, kiša	Meteorološki uslovi tokom trke.
Istorijske i izvedene	vreme pobednika prošle godine, prosečna pozicija (poslednjih 5 trka), broj odustajanja (poslednjih 5 trka), dobijene/izgubljene pozicije (poslednjih 5 trka), prosek trajanja zamene guma po timu (poslednjih 5 trka), prosečno vreme koje se izgubi prilikom zamene guma (na jednoj stazi), broj stajanja na stazi u prethodnoj godini, broj preticanja po vozaču na istoj stazi u prošloj sezoni, najbolje kvalifikaciono vreme vozača	Karakteristike izvedene iz istorijskih i agregiranih podataka.

Tabela 1: Karakteristike korišćene prilikom treniranja modela

Na slici 1 prikazana je matrica korelacije karakteristika definisanih u tabeli 1. Većina karakteristika nema izraženu međusodnu korelaciju. Jaka negativna korelacija prisutna je kod karakteristika koje opisuju broj krugova i dužinu staze jer dužina Velike nagrade iznosi najmanje 300km, sa izuzetkom Velike nagrade Monaka. Jaka pozitivna korelacija uočava se između početne pozicije vozača i rezultata na kraju trke.

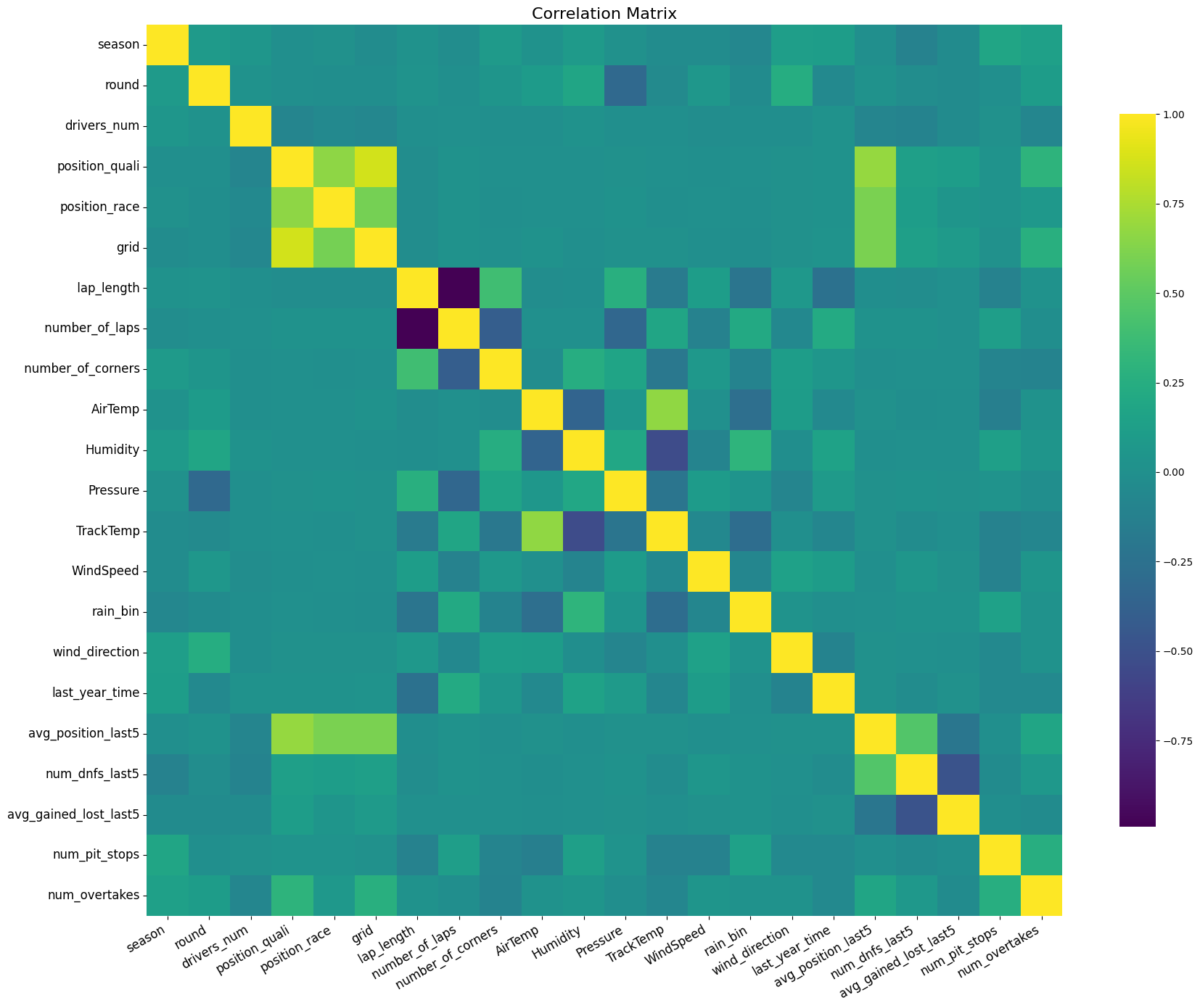
Slika 1: Matrica korelacije korišćenih karakteristika

2.2.Metrike

2.2.1.NDCG – Normalized Discounted Cumulative Gain

NDCG je mera kvaliteta rangiranja koja opisuje koliko uspešno algoritam rangira stavke prema njihovoj relevantnosti. Osnovna ideja iza ove metrike je da su greške na višim pozicijama (tj. na vrhu liste) značajnije nego greške na nižim pozicijama. Ukoliko model rangira manje relevantne stavke visoko, metrika će kazniti takvo ponašanje više nego ako su te greške pri dnu.

Ova vrednost se računa kroz tri etape:

1. Discounted Cumulative Gain (DCG) se računa kao:

$$ \begin{aligned} DCG_k = \sum_{i=1}^{k} \frac{rel_i}{\log_2(i + 1)} \end{aligned}$$

Gde je:

• $rel_i$— relevantnost stavke na poziciji i (u ovom eksperimentu poziciji 1 odgovara vrednost 20, drugoj 19, a poslednjoj relevantnost 1)
• k — broj pozicija koje se uzimaju u obzir (u ovom eksperimentu uzima se vrednost 10, jer prvih 10 vozača dobija poene).

2. Ideal DCG (IDCG) predstavlja maksimalni mogući DCG za date relevantnosti, tj. vrednost DCG kada su stavke savršeno rangirane po relevantnosti.
3. Normalized DCG (NDCG) se definiše kao odnos ostvarenog DCG i idealnog DCG:

$$\begin{aligned} NDCG_k = \frac{DCG_k}{IDCG_k} \end{aligned}$$

Vrednosti ove metrike su u intervalu [0, 1], gde 1 označava savršeno rangiranje, dok vrednosti bliže 0 označavaju loše performanse algoritma rangiranja.

2.2.2.Kendall’s 𝜏

Kendall’s 𝜏 je statistička mera koja procenjuje sličnost između dva rangiranja. Zasniva se na broju saglasnih (konkordantnih) i nesaglasnih (diskordantnih) parova u dva poređenja. Za niz od n elemenata, Kendall’s 𝜏 se računa kao:

$$\begin{aligned} \tau = \frac{C - D}{\frac{n(n - 1)}{2}} \end{aligned}$$

gde su:

• C — broj konkordantnih parova,
• D — broj diskordantnih parova.

Vrednosti 𝜏 se kreću u opsegu [-1, 1], gde 1 označava savršeno slaganje rangova, 0 odsustvo korelacije, a -1 potpuno obrnut redosled.

2.2.3.Spearmanov rang korelacije

Spearmanova korelacija meri koliko su dva rangiranja slična. Umesto da gleda stvarne vrednosti, posmatra samo redosled elemenata.
Za niz od n elemenata, prvo se izračunaju razlike između rangova svakog elementa u dve liste, označene kao $d_i$.
Speranov rang korelacije se definiše kao:

$$\begin{aligned} \rho = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} \end{aligned}$$

Vrednosti ⍴ se kreću od -1 (obrnuti rangovi) do 1 (savršeno slaganje rangova), dok ⍴ = 0 označava odsustvo monotone veze.

2.2.4. Root Mean Squared Error (RMSE)

RMSE je standardna mera koja pokazuje prosečnu veličinu greške između stvarnih i predviđenih vrednosti. Izračunava se kao kvadratni koren prosečne kvadratne greške:

$$\begin{aligned} RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2} \end{aligned}$$

gde su:

• y — stvarna vrednost,
• $\hat{y}_i$ — predviđena vrednost,
• n — broj vozača.

Manja vrednost RMSE znači da su predviđanja bliža stvarnim vrednostima.

2.2.5 Mean Reciprocal Rank (MRR)

Mean Reciprocal Rank (MRR) može se koristiti u Formuli 1 da se oceni koliko dobro model predviđa pobednika trke. Ako je pravi pobednik visoko rangiran u listi predviđanja, doprinos MRR-u je veći. Formula glasi:

$$\begin{aligned} \text{MRR} = \frac{1}{|R|} \sum_{i=1}^{|R|} \frac{1}{\text{rank}_i} \end{aligned}$$

gde je $R$ skup trka, a $\text{rank}_i$ pozicija na kojoj je model rangirao stvarnog pobednika u trci $i$. Vrednosti ove metrike kreću se između 0 i 1. Vrednost 1 ukazuje da je pobednik svaki put pogođen, a vrednosti bliže nuli da je pobednik rangiran pri dnu liste.

2.3.Statističke metode

2.3.1. Linearna regresija

Linearna regresija predstavlja jednu od najosnovnijih statističkih i mašinskih metoda za modelovanje zavisnosti između jedne zavisne promenljive (target) i jedne ili više nezavisnih promenljivih (feature). Suština linearne regresije ogleda se u pretpostavci da postoji linearna veza između ulaznih karakteristika i izlazne vrednosti, koja se može opisati linearnom funkcijom oblika:

$$\begin{aligned}y = β₀ + β₁x₁ + β₂x₂ + … + β_n x_n \end{aligned}$$

gde su:

• y - predikcija zavisne promenljive
• $x₁, x₂, …, ​ x_n$ - nezavisne promenljive
• $β₀, β₁, β₂, …, β_n$ - parametri modela koji određuju značaj pojedinih faktora

U slučaju predviđanja rezultata trke Formule 1, linearna regresija se može koristiti u okviru pairwise pristupa, gde se vrše poređenja između parova vozača. Za svaki par vozača (i,j) formira se ulazni vektor razlika njihovih karakteristika, a model donosi odluku:

$$ \begin{aligned} fᵢⱼ = β₀ + β₁(xᵢ₁-xⱼ₁) + β₂(xᵢ₂−xⱼ₂) + … + βₙ(xᵢₙ−xⱼₙ) \end{aligned}$$

Na osnovu ove vrednosti donosi se binarna odluka:

• 1, ako vozač i završava ispred vozača j
• 0, ako vozač j završava ispred vozača i

Serijom ovakvih parnih poređenja između svih vozača u jednoj trci formira se konačna rang lista.

2.3.2. Support Vector Machine (SVM)

Support Vector Machine (SVM) predstavlja jednu od osnovnih metoda nadgledanog učenja koja se koristi za klasifikaciju i regresiju. SVM uči hiper-ravan koji najbolje razdvaja klase u prostoru karakteristika, maksimizujući marginu između podataka iz različitih klasa.

U slučaju predviđanja rezultata trke Formule 1, kao i kod linearne regresije, SVM se takođe može koristiti u okviru pairwise pristupa, gde se vrše poređenja između parova vozača. Za svaki par vozača (i,j) formira se ulazni vektor razlika njihovih karakteristika, a model donosi odluku:

$$\begin{aligned}fᵢⱼ = w · (xᵢ - xⱼ) + b\end{aligned}$$

gde su:

• w – vektor težina modela
• b - slobodni član
• xᵢ, xⱼ - vektori karakteristika vozača i i j

Na osnovu ove vrednosti donosi se binarna odluka, 1 ako vozač i završava ispred vozača j ili 0, ako vozač j završava ispred vozača i.

2.3.3. Naivini Bajes sa Laplasovim zaglađivanjem

Naivni Bajes je linearni probabilistički klasifikator koji se zasniva na Bajesovoj formuli verovatnoće hipoteze. Bajesova formula se zasniva na pretpostavci da slučajni događaji $H_1, H_2, …, H_n$ čine potpun sistem hipoteza, to jest da predstavljaju ceo prostor događaja i međusobno su disjunktni. Ako je A događaj za koji važi P(A) > 0, tada se verovatnoća da je hipoteza $H_i$ dovela do realizacije događaja A računa po formuli:

$$ \begin{aligned} P(H_i \mid A) = \frac{P(H_i) , P(A \mid H_i)}{P(A)}, \end{aligned}$$

gde je:

• $P(A)$ verovatnoća da se odigrao događaj A
• $P(H_i)$ verovatnća hipoteze $H_i$
• $P(A∣H_i)$ uslovna verovatnoća događaja A pod uslovom $H_i$
• $P(H_i|A)$ verovatnoća da je hipoteza $H_i$ dovela do realizacija događaja A

U ovom pristupu 70% podataka (103 trke) korišćeno je za trening, a 30% (45 trka) za testiranje. Kako je ova podela izvršena hronološki, neki vozači, staze i timovi su nepoznati modelu. Da bi se ovaj probem rešio, korišćeno je Laplasovo zagrađivanje (Laplace smoothening) koje je predstavljeno formulom:

$$ \begin{aligned} P(H_i \mid A) = \frac{P(H_i) , P(A \mid H_i) + \alpha}{P(A) + |V|}, \end{aligned}$$

gde je:

• α - korektivni faktor (u projektu iznosi 1)
• |V| - broj svih mogućih karakteristika (tim, vozač, vremenske prilike, staza…)

2.4.Duboka neuronska mreža

Duboke neuronske mreže (DNN) predstavljaju skup više slojeva povezanih neurona koji omogućavaju modelovanje složenih nelinearnih zavisnosti između ulaznih podataka i izlaza. One su posebno pogodne za zadatke gde interakcije između karakteristika nisu trivijalne i gde jednostavni linearni modeli ne mogu da uhvate skrivene obrasce u podacima.

Za preciznije predviđanje rezultata trka Formule 1 koristi se duboka neuronska mreža koja modeluje zavisnosti između karakteristika vozača i njihovog plasmana. Korišćena su dva pristupa. Prvi pristup je mreža koja kao ulaz dobija jednog od 20 vozača, a na izlazu daje verovatnoću da je taj vozač na vrhu liste. Na osnovu tih skorova se formira konačna rang-lista.

Pre nego što podatke prosledimo linearim slojevima, kategoričke vrednosti se prvo pretvaraju u numeričke pomoću embedding slojeva. Embedding sloj mapira svaku kategoriju na vektor realnih brojeva, omogućavajući linearnoj mreži da ih analizira i uči odnose između različitih kategorija. Kodiranje se radi pomoću factorize funkcije iz biblioteke pandas u Python-u, koja svakoj jedinstvenoj kategoriji dodeljuje jedinstveni ceo broj, čime se kategoričke vrednosti lako mogu proslediti embedding sloju.

Ova mreža sadrži više linearnih slojeva sa LeakyReLU aktivacijom, batch normalizacijom i dropout regularizacijom. Na slici 2 prikazana je precizna arhitektura mreže.

Slika 2: Arhitektura duboke neuralne mreže

Drugi pristup je mreža koja kao ulaz dobija parove vozača, a na izlazu daje predikciju koji je od njih bolji. Ova mreža sadrži tri linearna sloja sa ReLU aktivacijom, batch normalizacijom i dropout regularizacijom. Na slici 3 prikazana je precizna arhitektura ove mreže.

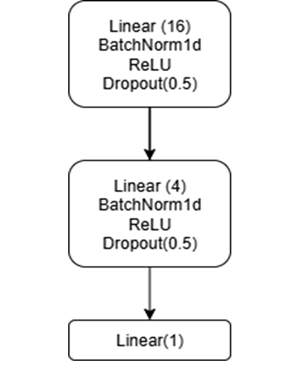Slika 3: Arhitektura duboke neuralne mreže za par po par pristup

2.5. Extreme Gradient Boosting - XGBoost

Gradijentno pojačavanje (gradient boosting) je tehnika mašinskog učenja koja kombinovanjem više slabih modela kreira jedan jak prediktivni model. Zadatak svakog od modela (sem prvog) je da ispravi greške prethodnog. Na kraju, sve male odluke se spajaju u jednu jaku i tačnu predikciju. XGBoost predstavlja primenjivanje ove tehnike nad stablima odlučivanja. Počinjemo od jednog slabog modela koji se naziva osnovni model. Potom se stabla dodaju jedno po jedno. Algoritam računa reziduale, odstupanja, predikcije svakog stabla. Svi reziduali se kombinuju i na osnovu loss funkcije se ocenjuje model. Kako bi se minimizovala funkcija gubitka, koristi se gradijentni spust. Neki hiperparametri (parametri čija se vrednost ne menja u toku treninga) XGBoost-a su stopa učenja 𝜂, broj stabala, maksimalna dubina stabla i 𝛾.
Stopa učenja označava koliko će se parametri modela menjati u jednoj iteraciji. Prevelika stopa učenja za posledicu može imati preskakanje minimuma funkcije gubitka. S druge strane, premala stopa učenja može dovesti do prespore konvergencije ili zaustavljanja na nekom lokalnom minimumu, ali ne na globalnom minimumu funkcije.
Broj stabala predstavlja broj slabih modela koji će se trenirati. Mali broj stabala donosi brže treniranje, ali model može biti previše jednostavan. Nasuprot tome, veliki broj stabala može da uči kompleksne obrasce, ali donosi i rizik od prenaučenosti (overfitting). Obično se ova vrednost ne podešava ručno, već se trening zaustavlja kada metrika na validacionom skupu prestane da se poboljšava.
Maksimalna dubina stabla je broj nivoa od korena do lista stabla. Kao i kod broja stabala, male vrednosti daju modele koji su sposobniji za generalizaciju, ali možda neće moći da pronađu kompleksnije obrasce, a velike vrednosti povećavaju rizik od prenaučenosti.
Hiperparametar 𝛾 kontroliše da li će se stablo deliti u nekom čvoru. Ukoliko taj čvor donosi veće smanjenje loss funkcije od zadate vrednosti, stablo će se granati, u suprotnom, na tom mestu ne postoji čvor.
Model XGBoost je implementiran kroz xgboost biblioteku u Python-u. XGBoost je implematiran sa dve različite ciljne funkcije NDCG i pairwise. Ciljna funkcija NDCG podrazumeva da model optimizuje loss koji aproksimira ovu metriku diferencijabilnom funkcijom. Rangiranje korišćenjem ciljne funkcije pairwise podrazumeva da model predviđa koji vozač će ostvariti bolji plasman za svaki par vozača.
Za optimizaciju hiperparametara korišćena je biblioteka Optuna, koja primenjuje princip Bajesove optimizacije kroz algoritam Tree-structured Parzen Estimator (TPE). Umesto pretraživanja celog prostora parametara (kao što je to slučaj kod grid search-a) koji može imati hiljade kombinacija, Optuna bira vrednosti hiperparametara na osnovu prethodnih evaluacija modela, kako bi ubrzala pronalaženje optimalne konfiguracije. Tokom procesa, Optuna trenira model sa različitim skupovima hiperparametara, evaluira performanse na validacionom skupu (korišćenjem NDCG metrike) i iterativno usmerava potragu ka kombinacijama koje imaju najveći potencijal za dobar rezultat. Optimalne vrednosti nekih hiperparametara pronađene pomoću ove biblioteke su prikazane u tabeli 2.

Hiperparametar	XGBoost - NDCG	XGBoost - pairwise
stopa učenja 𝜂	0,22887	0,29822
maksimalna dubina stabla	7	9
parametar 𝛾	0,21104	0,47453

Tabela 2: Neki od hiperparametara za XGBoost model

2.6. Problem hronološke podele podataka

U mašinskom učenju vrlo često podela podataka na set za treniranje, validaciju i test vrši se nasumično. Međutim, u ovom radu situacija je drugačija. Formula 1 je sport koji se vrlo brzo menja. Promena pravila, razvoj bolida, sticanje iskustva samo su neki od faktora koji utiču na rezultate. Sve ove kategorije su promenljive u vremenu. Stoga, treba voditi računa da se skup podataka hronološki podeli. Najjednostavniji pristup bio bi da se prvih 70% posto trka koristi za treniranje narednih 10% za validaciju i preostalih 20% za testiranje. Ovakav pristup donosi brojna ograničenja. Pre svega, evolucija koja se dešava kroz sezone obuhvaćene validacijom i treningom. Sezone do 2020. sa sobom nose i dominaciju Mercedesa. Učeći na ovakvim podacima, model može da nauči da je vozač Mercedesa, ako ne na prvom mestu, onda gotovo sigurno na pobedničkom postolju. Ovo predstavlja naročito veliki problem, jer je na primer od 2021. do sredine 2024. Red Bull bio dominantan.

2.7. Rolling window tehnika i XGBoost

Ovaj problem se može rešavati korišćenjem Rolling window tehnike. Ona podrazumeva podelu skupa podataka na manje vremenske okvire. Postoje dva pristupa. U oba se počinje od najstarijih podataka, i oni koji slede predstavljaju podatke za testiranje. Slika 4 prikazuje da prvi pristup podrazumeva pomeranje okvira za testiranje podataka ka novijim podacima. Drugi način je da se okvir proširuje, na primer počinjemo od cele 2018. sezone, i postepeno proširujemo da okvir uključuje sve do pete trke pred kraj 2024, a tih preostalih 5 koristimo kao test set. U ovom projektu tehnika Rolling window se kombinuje sa modelom XGBoost. Veličina prozora je konstantna i iznosi 30 trka, validacija se vršila na 2, a test na 4 trke. U svakoj iteraciji prozor se pomerao za 6 trka.

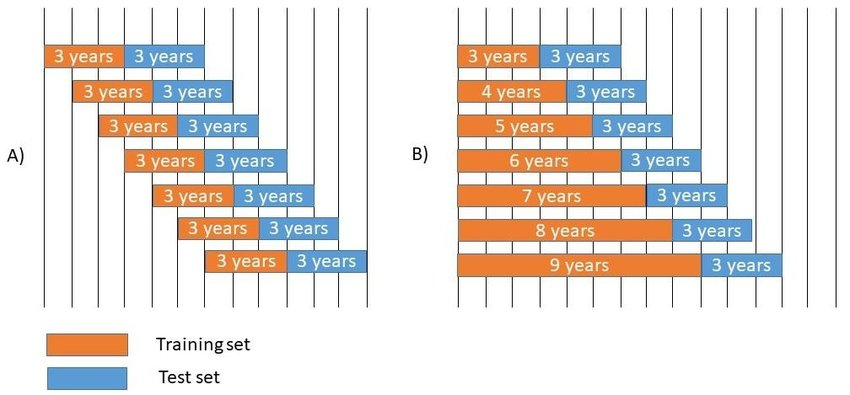
Slika 4: Prikaz Rolling window tehnike

2.8. XGBoost sa pairwise treniranjem

Pored ugrađenog pairwise pristupa u XGBoost-u, isproban je još jedan pristup koji se zasniva na manuelnom treniranju nad parovima. Dok pomenut ugrađeni pairwise interno kreira sve parove unutar definisanih grupa i optimizuje rang direktno na nivou instanci, manuelni pairwise pristup zahteva da se parovi eksplicitno generišu, pri čemu se model trenira kao binarni klasifikator nad odnosom između članova para. Glavna razlika između ova dva pristupa leži u načinu kreiranja parova i funkciji gubitka: XGBoost automatski upravlja parovima i koristi pairwise log loss, dok manuelni pristup koristi standardni binary log loss i zahteva dodatnu obradu kako bi se predikcije po parovima transformisale u konačni rang.

3. Rezultati

3.1 Performanse modela

Model	NDCG	Kendall’s τ	Sperman	RMSE	Pairwise tačnost
Linearna regresija	-	-	-	-	80,1%
SVM	-	-	-	-	82,8%
Naivini Bajes	0,6818	0,1329	0,1829	7,2450	-
XGBoost - pairwise	0,9619	0,5753	0,7241	4,0755	-
XGBoost - NDCG	0,9586	0,5694	0,7048	4,3400	-
XGBoost - Rolling window	-	-	-	-	-
DNN	0,73	-	-	-	-
DNN - pairwise	-	-	-	-	74,5%
XGBoost - treniranje nad parovima	0,987	0,86	0,92	1,58	-

Tabela 3: Uporedni prikaz metrika za različite modele

3.2. Statistički modeli

Na slikama 5, 6 i 7 prikazani su rezultati predikcije plasmana vozača u test skupu trka koristeći tri pomenuta statistička modela. Slika 5 prikazuje rezultate linearne regresije primenjene u pairwise pristupu. Slika 6 prikazuje rezultate dobijene korišćenjem SVM-a, takođe u pairwise pristupu.

Slika 5: Konfuziona matrica linearne regresije Slika 6: Konfuziona matrica SVM

Model linearne regresije daje tačnost 80,1%, a SVM 82,8%. Analizom ovih tačnosti i konfuzionih matrica može se uočiti da oba modela uspešno predviđaju relativni plasman u većini parova, ali retko uspevaju da precizno rekonstruišu tačan konačan plasman vozača.

Na slici 7 je prikazana matrica konfuzije kada je korišćen model Naivni Bajes sa Laplasovim zaglađenjem. Njenom analizom može se uočiti da glavna dijagonala nije izražena. Takođe, pobednik je ispravno predviđen svega 3 puta što ukazuje da model nema mogućnosti da generalizuje na novije podatke. Ovakvo ponašanje je očekivano jer je Formula 1 veoma dinamičan sport i neophodni su kompleksniji modeli koji mogu da prate zavisnost plasmana od vremeskih uslova i konfiguracije staze, kao i evoluciju timova i vozača. Vrednosti metrika iz tabele 3 ukazuju da ovaj model jako loše rangira vozače, u proseku sa greškom većom od 7 pozicija.

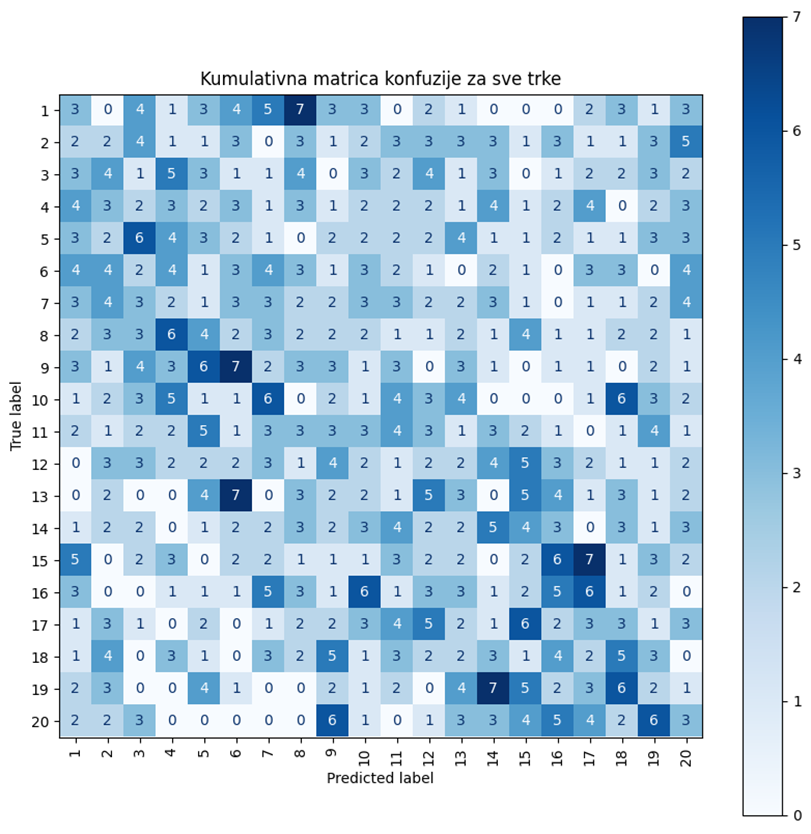Slika 7: Matrica konfuzije za model naivni Bajes sa Laplasovim zaglađenjem

3.3. Duboka neuralna mreža

Za treniranje mreže nad svih 20 vozača po trci korišćen je Stochastic Gradient Descent SGD optimizator i ListNetLoss funkcija gubitka, specijalno dizajnirana za zadatke rangiranja. Na slici 8 prikazani su grafikoni gubitka i NDCG metrike kroz epohe.

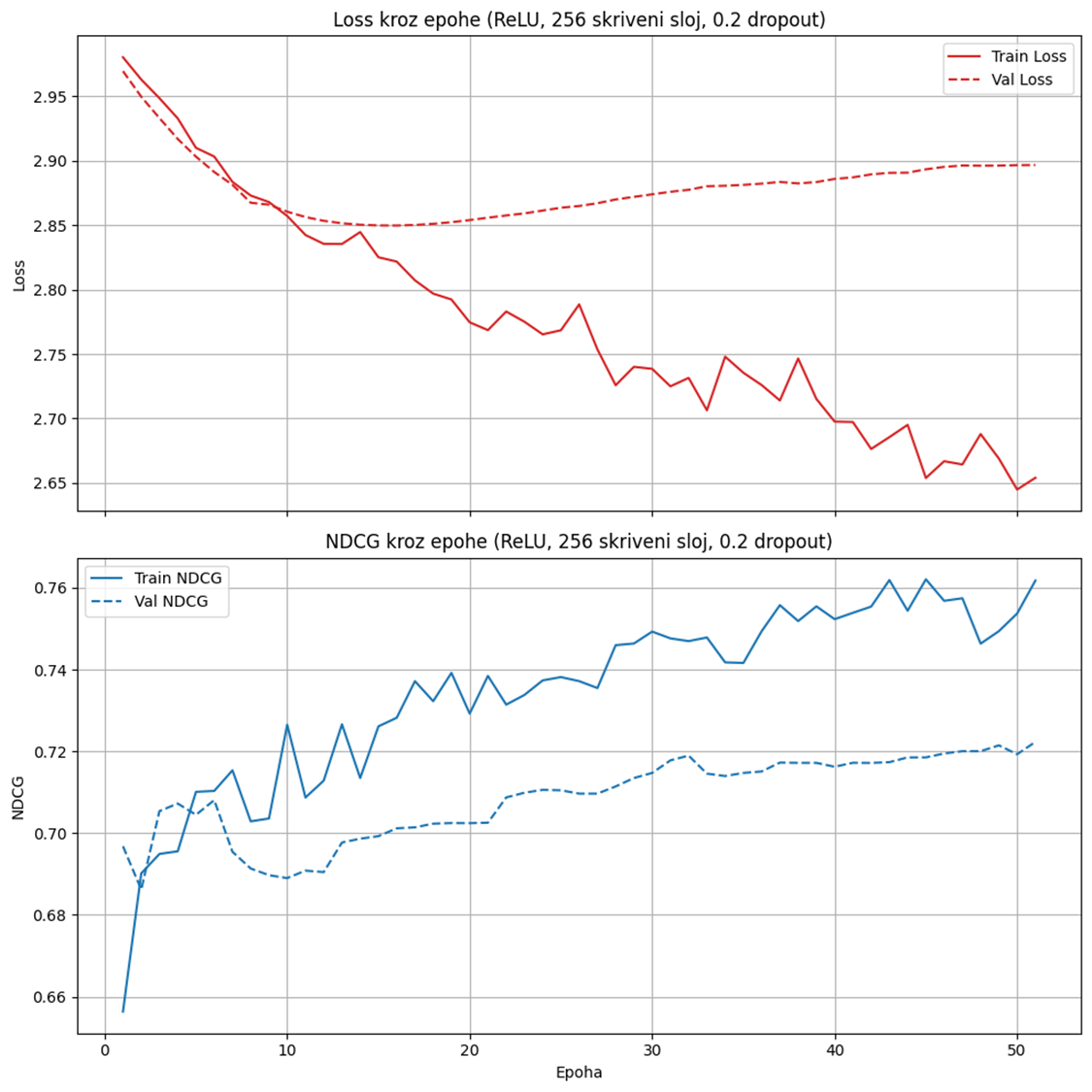Slika 8 : Gubitak i NDCG kroz epohe tokom treniranja duboke neuralne mreže

Za treniranje druge mreže nad parovima vozača korišćen je Adam optimizator i Binary Cross-entropy Loss With Logits funkcija gubitka. Ova funkcija gubitka kombinuje sigmoid aktivaciju i standardni binary cross-entropy, tako da model direktno uči verovatnoću da je jedna instanca u paru rangirana više od druge. Ovakav pairwise pristup dubokoj neuralnoj mreži dao je 74,5% tačnosti.

3.4. XGBoost

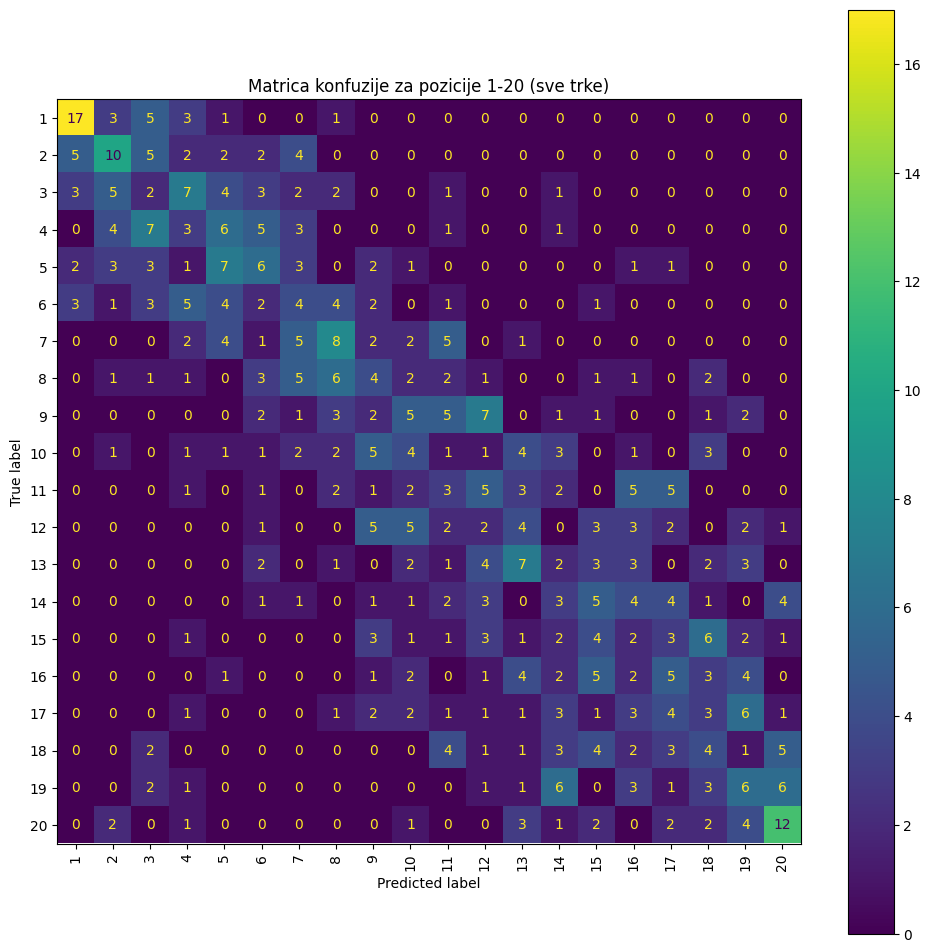Slika 9: Matica konfuzije za XGBoost sa pairwise cljnom funkcijom
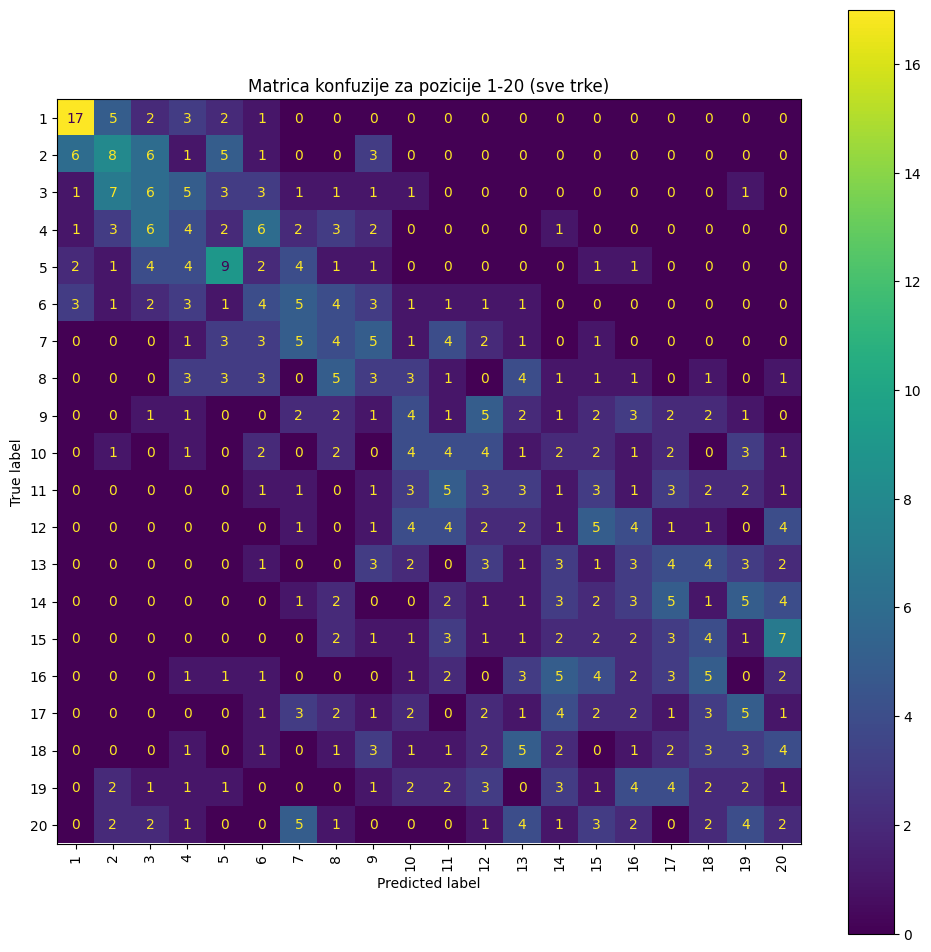
Slika 10: Matica konfuzije za XGBoost sa NDCG cljnom funkcijom

Na slici 10 prikazane su matrice konfuzije kada je XGBoost treniran sa ciljnom funkcijom NDCG i na slici 9 kada je korišćena ciljna funkcija pairwise. Na osnovu ovih konfuzionih matrica može se zaključiti da pairwise pristup daje izraženiju dijagonalu. Ovo je očekivano jer NDCG prioritizuje tačno rangiranje prvih 10 vozača, dok pairwise pristup bolje opisuje pojedinačne rezultate među vozačima. Oba modela su tačno predvidela pobednika u 17 trka, dok sa pairwise ciljnom funkcijom model bolje predviđa i drugo mesto (10 pogođenih nasuprot 8). Sve metrike prikazane u tabeli 3 ukazuju na značajno bolje performanse ovih modela u poređenju sa statističkom analizom.

3.5. Rolling window tehnika i XGBoost

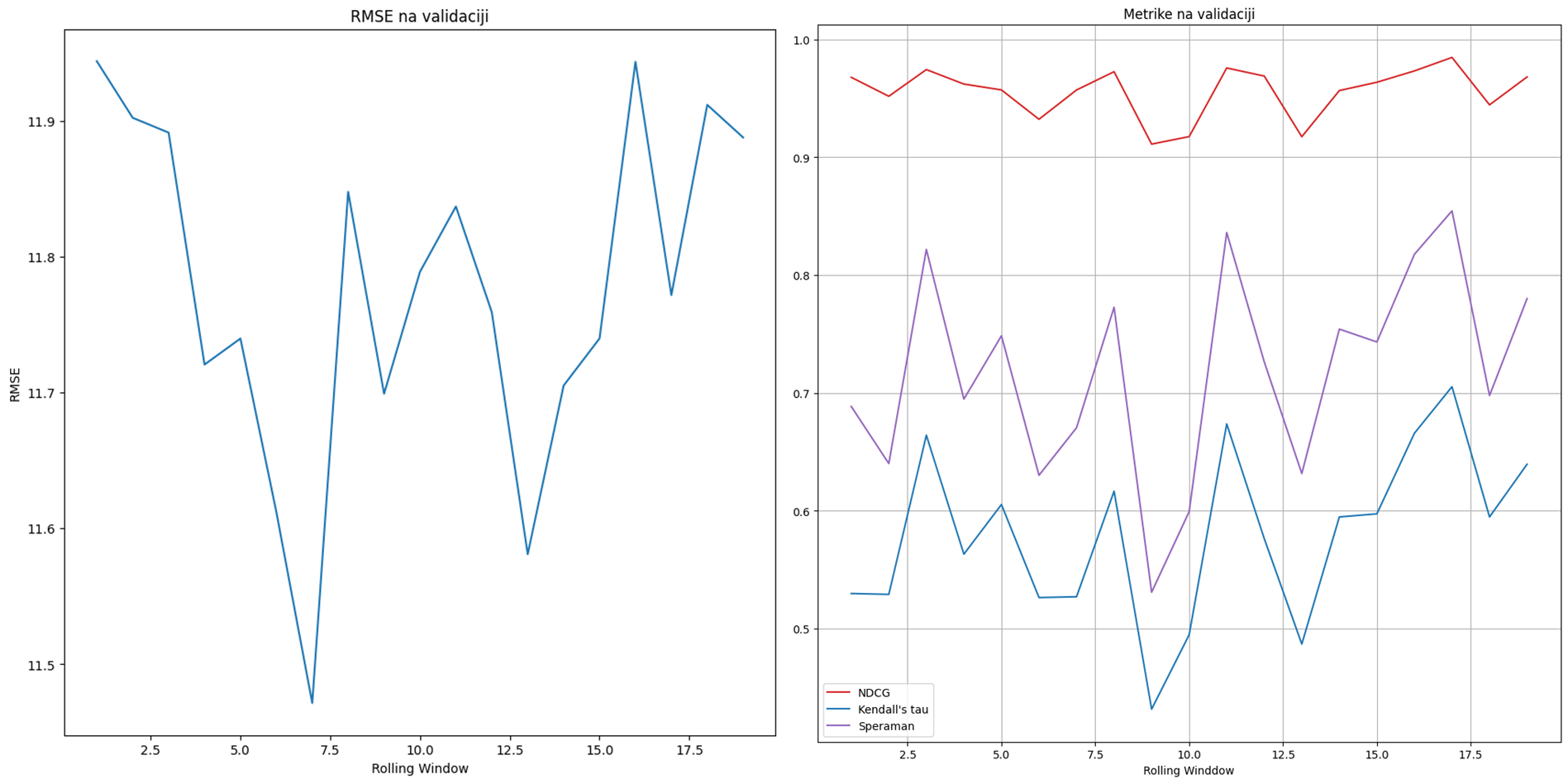Slika 11: Prikaz vrednosti metrika (NDCG, Kendall’s τ i Spermanov rang korelacijie) na validaciji (levo) i vredvosti RMSE na validaciji (desno)

Na slici 11 prikazane su vrednosti metrika na validaciji (NDCG, Kendall’s τ i Spermanov rang korelacijie) i vrednosti RMSE. Primećuje se da se metrike ne poboljšavaju. NDCG veoma malo osciluje sa vrednostima između 0,9 i 1. Kod vrednosti Kendall’s τ i Spermanovog ranga korelacijie javljaju se veliki padovi. Takođe, RMSE se ne spušta ispod 11 što ukazuje da model u proseku pravi grešku od 11 pozicija pri rangiranju vozača. Kako nije primećen rastući trend za metrike na validaciji, odnosno opadajući za RMSE, za ovaj metod nije vršeno testiranje. Korišćenjem Rolling window tehnike prethodna stabla se ne modifikuju, već se na prethodna stabla dodaju se nova. Ova osobina XGBoost algoritma dovodi do prenaučavanja i slabijih prediktivnih sposobnosti, zbog čega metod nije dao zadovoljavajuće rezultate.

3.6. XGBoost sa pairwise treniranjem

Na slici 12 prikazana je konfuziona matrica XGBoost-a treniranog na ručno formiranim parovima.
Slika 12: Konfuziona matrica XGBoost-a treniranog na ručno formiranim parovima

Vrednosti metrika su prikazane u tabeli 3. Pored ovih računata je i metrika Mean Reciprocal Rank (MRR) koja iznosi 0,89. Kako je ova metrika veoma blizu 1 može se zaključiti da model jako dobro predviđa poziciju pobdnika. Vrednost RMSE iznosi 1,58 što ukazuje da model pravi jako mala odsupanja u rangovima vozača. Metrika NDCG ukazuje da model dobro rangira vrh liste, dok Kendall’s τ i Spermanov rang korelacije pokazuju da postoji jaka pozitivna povezanost između predikcija i stvarnog ranga.

4. Diskusija

Statistički metodi nisu dali zadovoljavajuće rezultate zbog svoje suviše jednostavne prirode. Duboka neuralna mreža (DNN) trenirana da predvidi celu rang-listu pokazala se neuspešnom, pre svega zato što korišćena funkcija gubitka nije bila adekvatna za taj zadatak. XGBoost i DNN model treniran da predvidi koji je od dva vozača bolji daju znatno bolje rezultate. Sa druge strane, Rolling Window pristup zasnovan na XGBoost modelu pokazivao je izraženo overfitovanje, što je ograničilo njegovu praktičnu primenu. Kao najefikasniji pristup pokazao se XGBoost sa treniranjem par po par.

4.1. Predlozi poboljšanja

Metrike ukazuju na postojanje prostora za poboljšanje. Moguća unapređenja uključuju dodavanje novih karakteristika koje dodatno opisuju kontekst trke: istorijski rezultati vozača na određenoj stazi, kao i performanse u specifičnim vremenskim uslovima (npr. pojedini vozači postižu značajno bolje rezultate u kišnim uslovima). Iako u ovom projektu stariji podaci nisu korišćeni, oni bi mogli da daju kontekst modelu o funkcionisanju sporta, a na novijim podacima bi mogao da se finetune-uje. Prikupljanje novih podataka i inženjering karakteristika bi omogućili i korišćenje složenijih modela, poput mreža za obradu vremenskih sekvenci, kao što su rekurentne neuralne mreže (RNN), Long-Short Term Memory (LSTM) mreže i transformeri, koji bi znatno poboljšali predviđanja.

5. Zaključak

Statističke metode su bile previše jednostavne da bi davale kvalitetna predviđanja. DNN treniran na celoj listi nije dao dobre rezultate jer arhitektura i loss funkcija nisu bile usklađene. Takođe, DNN treniran na parovima nije ostvario zadovoljavajuće pairwise performanse, pa nije dalje testiran na ostalim metrike.

XGBoost treniran nad ručno podeljenim parovima dao je najbolje rezultate. Pristup sa rolling window nije bio uspešan, jer vrlo brzo dolazi do overfitovanja jer stabla se ne ažuriraju već se samo dodaju nova.

Literatura

[1] Kike FRANSSEN. COMPARISON OF NEURAL NETWORK ARCHITECTURES IN RA-
CE PREDICTION Predicting the racing outcomes of the 2021 Formula 1 season. Master’s
thesis, Tilburg University, 2022.

[2] Octaviana-Alexandra Cheteles. Feature importance versus feature selection in predictive
modeling for formula 1 race standings. B.S. thesis, University of Twente, 2024.