Играње шаха помоћу учења поткрепљивањем

Аутори:

Вељко Галовић, ученик II разреда Гимназије „Вељко Петровић” у Сомбору

Павле Ивановић, ученик IV разреда Математичке гимназије у Београду

Ментори:

Наташа Јовановић, EPFL у Лозани

Милица Гоjак, Електротехнички факултет у Београду

Матеја Стојковић, Електротехнички факултет у Београду

Апстракт

Овај пројекат је развио и евалуирао неколико приступа заснованих на неуронским мрежама за шаховски ВИ (вештачка интелигенција), експериментишући са учењем имитације од Stockfish-а, ResNet мрежама за одабир потеза и вредновање позиције, посебном евалуационом мрежом упареном са minimax претрагом, MCTS (Монте Карло претрага стабла) методом са самосталним играњем, и на крају са евалуатором у NNUE стилу. Прикупљене су обимне количине података за тренирање (Lichess база и партије само-игре), имплементирани су процеси обраде података за FEN позиције са Stockfish евалуацијама и најбољим потезима, а модели су итеративно тренирани уз мерење валидационе тачности, средње квадратне грешке евалуационе главе и практичне снаге игре. Кључни резултати: (1) први двоглави и ResNet модели показали су ограничено побољшање у односу на насумичну игру; (2) модел заснован искључиво на евалуацији у комбинацији са minimax-ом дао је најперспективније понашање у игри, али је био спор; (3) NNUE тренирање је у раним епохама показало нестабилне метрике и захтева додатно подешавање и рачунске ресурсе.

Abstract

This project developed and evaluated several neural-network-based approaches for a Chess AI, experimenting with imitation learning from Stockfish, ResNet-based policy/value networks, a separate evaluation network paired with minimax search, Monte Carlo Tree Search (MCTS) with self-play, and finally an NNUE-style evaluator. Large-scale training data (Lichess database and self-play) was collected, data pipelines for FEN-encoded positions with Stockfish evaluations and best moves were implemented, and models were iteratively trained while measuring validation accuracy, evaluation-head mean-square error and practical playing strength. Key outcomes: (1) early two-headed and ResNet models showed limited improvement over random play; (2) an evaluation-only model combined with minimax produced the most promising playing behavior but was slow; (3) NNUE training produced unstable metrics in early epochs and requires further tuning and compute.

1. Увод

Шах је једна од најпознатијих друштевних игара, поготово за људе који желе да тестирају своје способности апстрактног размишљања. Од настанка рачунарства као научне дисциплине, шах је служио као велика инспирација за развој вештачке интелигенције. То је кулминирало у 1997. години, када је по први пут рачунар победио тадашњег светског првака у шаху¹. Од тог тренутка, најбољи играчи шаха су управо компјутери, и задатак је постао развити најбољег шаховског компјутера. Све до 2017. године доминирали су компјутери засновани на ефикасном калкулисању што је могуће више потеза унапред када је свет компјутерског шаха доживео препород појавом AlphaZero-а². Након само 9 сати тренирања, победио је тадашњи најбољи шаховски компјутера Stockfish 8³ убедљивим резултатом од 28 победа, 72 ремија и 0 пораза, користећи потпуно нови приступ. Такав догађај служи као доказ да и даље постоји много тога што не знамо о шаху као игри, и као инспирација за даљи рад и развој.

Циљ пројекта јесте развитак шаховског компјутера, по угледу на најбоље комјутере садашњице. У оквиру овог рада испробано је више приступа: имитационо учење над Stockfish-овим потезима, ResNet-двоглави модел (oдабир потеза и евалуацијa позицијa), засебан евалуациони модел са minimax алгоритмом, модел заснован на MCTS (Monte Carlo Tree Search) са само-игром и на крају NNUE (Efficiently Updatable Neural Network). Ниједан од модела нема претходно знање о правилима шаха. Током рада коришћена је комбинација јавнo доступнe базe података партија одиграних на сајту Lichess.org⁴, база података мајсторских партија, као и генерисаних позиција од стране модела током игре сам против себе.

2. Метод

2.1. Скуп података

Основа сваког пројекта из вештачке интелигенције јесте добар скуп података. За потребе шаховске ВИ-е прикупљени су подаци из три извора. Први извор података био је база мајсторских партијa⁴ са Lichess платформе. Будући да се шаховске партије састоје из више позиција (стања на табли), оне су подељење у засебне позиције којих је на крају било око милион. Испоставило се да је то премало позиција, те су узете партије са исте платформе, али из 2023. године. Партије су филтриране по рејтингу, а задржане само оне од играча чији је ELO (метрика шаховске вештине) >2000 и подељене на позиције, тако да укупан број позиција износи око 6,7 милиона позиција. Трећи извор података је био узет са GitHub странице пројекта AlphaZero², али су они били запаковани у затворени фајл систем .bagz који није било могуће дешифровати.

2.2. Кодирање информација са шаховске табле

Пре коришћења неуралних мрежа, неопходно је кодирати позиције и потезе, односно превести их у бројеве.

2.2.1. Кодирање табле

Две методе кодирања шаховске табле су коришћене.

1. Поједностављена AlphaZero метода²:

Позиција фигура на табли се кодира као тензор димензија $20 \times 8 \times 8$. Постоји 6 типова фигура у шаху (пијун, топ, скакач, ловац, дама и краљ) које могу припадати белом или црном играчу, а поред позиција фигура кодирају се и 8 мета-података о позицији: чији је потез, могућност мале и велике рокаде за оба играча, могућност ан пасана, правило 50 потеза⁵ и укупан број потеза. AlphaZero поред наведеног, у свом кодирању садржи последњих 7 позиција у игри. Како би се умањила комплексност кодирања и начина прављења података, одлучено је да се користи само тренутна позиција.

Индекс прве димензије	Енкодирана информација
0-11	Позиције фигура на табли
12	Чији је потез
13	Могућност мале рокаде за белог
14	Могућност велике рокаде за црног
15	Могућност мале рокаде за црног
16	Могућност велике рокаде за црног
17	Да ли постоји легалан ан пасан
18	Правило 50 потеза
19	Укупан број потеза / 100

2. HalfKP метода:

За NNUE мрежу коришћен је начин кодирања дефинисан специјално за њу. Такозвани HalfKP⁶ (Half King-Piece) начин кодирања позиције, као што само име каже, гледа однос позиције краља играча који је на потезу, и позиције сваког од 10 преосталих фигура на табли (изузимајући краљеве). Позиција се на такав начин кодира у низ дугачак 40960 ($=64 \times 64 \times 10$) битова, прва димензија говори о позицији краља, друга о позицији фигуре, и трећа о типу фигуре. Ако се посматра почетна позиција у шаху, то у пракси изгледа овако:
Свој краљ на а1, свој пијун на а1: 0
Свој краљ на а1, свој пијун на а2: 0
…
Свој краљ на е1, свој пијун на а2: 1
Свој краљ на е1, свој пијун на а3: 0
…
итд.

Иако је ова метода кодирања позиције пре свега заснована на игри шоги, где су правила знатно другачија од шаха, у пракси је примећено да одлично ради и за шах. Могу се приметити пар својстава које су згодне за шах.

• Позиције које се огледају у огледалу имају истe улазнe вредности, јер се посматра позиција из перспективе играча који је на потезу, без обзира на боју. Ово својство биће искоришћено касније.

• У отварању и средишњици краљ се у поређењу са осталим фигурама помера веома ретко, тако да се једним потезом мења само неколико битова у улазу. На пример, узимајући почетну позицију и први потез скакач c3, потребно је само променити следеће битове:

  • Свој краљ на e1, свој скакач на b1: 1 → 0
  • Свој краљ на e1, свој скакач на c3: 0 → 1
  • Противнички краљ на e8, свој скакач на b1: 1 → 0
  • Противнички краљ на e8, свој скакач на c3: 0 → 1

  Ово је разлог иза имена NNUE, односно Efficiently Updatable Neural Network.

2.2.2. Кодирање потеза

Коришћен је начин кодирања потеза који је користио Гугл током свог развоја AlphaZero², а то је тензор димензија $8 \times 8 \times 73$. Посматра се са ког поља „започиње потез”, дакле $8 \times 8$ могућих поља. Поред тога, првих 56 равни треће димензије представљају теоретски могуће потезе „као краљица”, следећих 8 представљају теоретски могуће потезе „као скакач”, и последњих 9 могуће подпромоције, у скакача, ловца, или топа. Важно је напоменути да се потези ловца, топа или краља могу представити у првих 56 равни.

2.3. Модели

Развијено је и имплементирано 5 различитих модела за сврху овог пројекта. У појединим моделима, излаз мреже представља полису, односно одговор на питање који је најбољи потез за дату позицију, док је у осталим евалуација позиције, тј. бројевна вредност у интервалу [-1, 1]. Ако је евалуација позитивна, то значи да је бели играч у предности, обрнуто за црног играча. Апсолутна вредност евалуације представља колико је тај играч у предности.
Ниједан од модела нема претходно знање о правилима шаха, већ само на основу података подешава параметре мреже и на такав начин учи да игра шах.

2.3.1. ResNet модел

ResNet модел користи резидуалне блокове⁷.

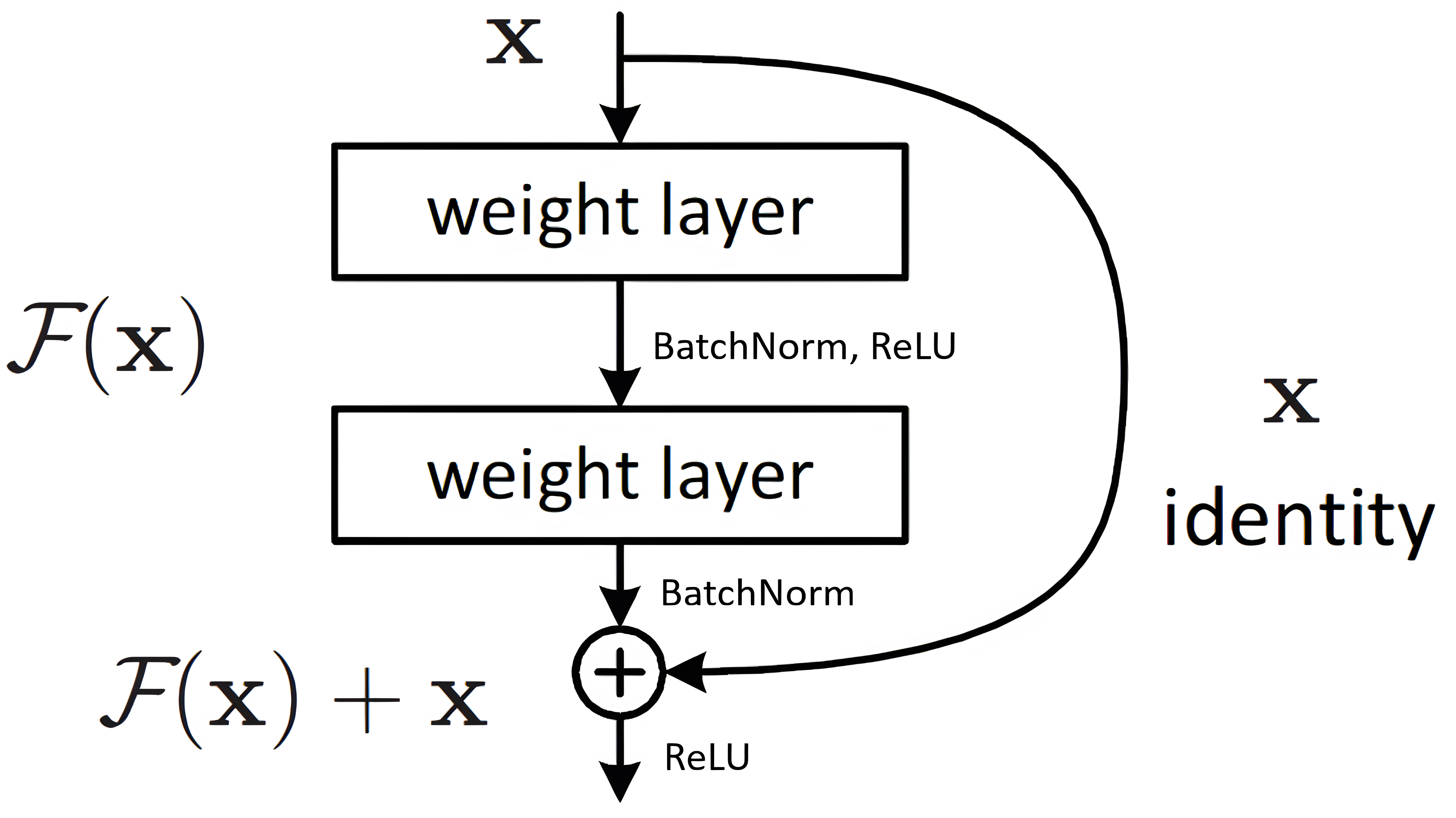
На слици 1 се може видети како функционише један резидуалан блок. Након више густо повезаних слојева и њихових активационих функција, њихов крајњи излаз се сабира са улазом и прослеђује следећем слоју.
Мотивација иза коришћења резидуалних блокова јесте спречавање проблема нестајућих градијената⁸ где последњи слојеви мреже веома мало утичу на сам излаз. Комплетна архитектура мреже се може видети на слици 2.

Улаз је кодирана позиција, а излаз представља низ од 4672 неурона који представља вероватноће за сваки од могућих потеза да је најбољи. Модел одиграва потез са највећом вероватноћом. Ако тај потез није легалан, бира се следећи најбољи, све док се не дође до легалног потеза.

2.3.2. Модел „Две главе”

Архитектура овог модела није знатно различита од мреже ResNet. И даље се користе резидуални блокови, али главна разлика је у томе што се сада главни део мреже рачва на два типа излаза: полису, односно најбољи потез, и евалуацију позиције.

2.3.3. MCTS / самоигра

AlphaZero је мрежа заснована на овој архитектури, и главна инспирација иза овог пројекта.

Главни проблем за сваког модела који игра шах јесу управо велике количине података које су неопходне за квалитетно и смислено учење. Овај приступ покушава да реши тај проблем на врло, наизглед, очигледан начин; то је генерисање тренинг података из партија у којима модел игра сам против себе. Алгоритам који је у центру овог модела јесте Монте Карло претрага стабла⁹. Чворови стабла представљају позиције на табли, а ивице одигране потезе. Постоје 4 фазе претраге, односно симулације, које се понављају одређени број пута.

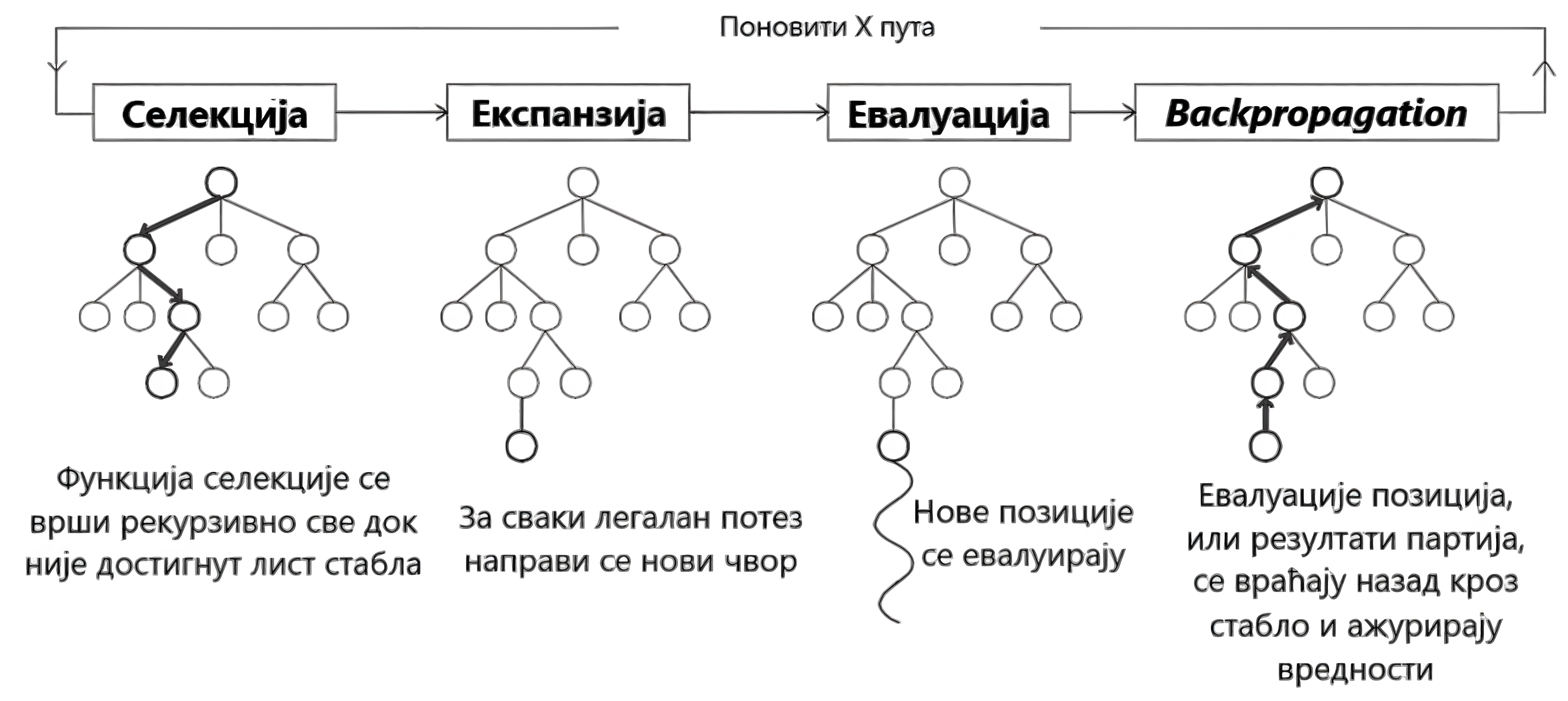
Селекција

Ова фаза представља пролазак од корена стабла (позиција над којој се врши евалуација), све до листа стабла. Овај процес се одвија тако што се бира најбоља ивица за сваки посећени чвор. Свака ивица поседује UCB (Upper Confidence Bound) вредност, којом се одређује најбоља ивица. UCB вредност ивице је збир вредности експлоатације и вредности истраживања. Наравно, пожељно је експлоатисати потезе који су већ познати да су добри, а у исто време постоји могућност постојања још бољег потеза који није још пронађен. Вредност експлоатације се рачуна на основу Q вредности, тј. просечне вредности ивице која се рачуна на основу евалуације неуралне мреже. Вредност истраживања се рачуна следећом формулом:

$$ E = \frac{c \cdot p \cdot v_{parent}}{1 + v_{edge}}, $$

где је $E$ вредност истраживања, $c$ параметар истраживања (коришћено је $c = 1$), $p$ излаз из неуралне мреже за тај потез, $v_{parent}$ број посећивања родитељског чвора и $v_{edge}$ број посећивања саме ивице.
Током проласка, памти се низ ивица од корена до листа, зарад последње фазе.

Експанзија

Када је лист стабла достигнут, и није у питању крај партије, он се проширује, тако што му се додаје по ивица за сваки легалан потез у тој позицији. Неурална мрежа доставља вероватноће за сваки потез.

Евалуација (симулација)

У овој имплементацији, пошто би било преспоро за услове у којима је рађено да се ради класична насумична симулација партије до краја, се за сваку од нових позиција прослеђује евалуација позиције неуралне мреже, осим ако је крај партије у питању; у том случају, за победу се прослеђује вредност од 1, за пораз -1, а за реми 0.

Повратно гурање (Backpropagation)

У овој фази се ажурирају ивице који се налазе у путањи до листа новодобијеним информацијама. Ажурирају се број посета и бројевна вредност ивица и чворова. Битно је напоменути да је неопходно обрнути знак након сваке ивице, како би вредност тачно одражавала перспективу одговарајућег играча.

Када се заврши одређен број симулација, у овом случају само 10, бира се ивица са највећим бројем посета. Коришћен је модел „Две главе”, јер су били потребни и евалуација позиције и вероватноће за потезе.

2.3.4. Модел ексклузивне евалуације

Пошто се приступ базиран на MCTS алгоритму није показао као добар због хардверских ограничености, следећи најлогичнији корак је био упростити га. Приступ који је заменио MCTS користи minimax алгоритам са алфа-бета орезивањем¹⁰ и евалуациону функцију како би одредио следећи потез. За евалуациону функцију искористили смо модел ексклузивне евалуације — модел који користи конволуционе и резидуалне блокове како би одредио дистрибуцију вероватноће потеза. Овај модел је трениран тако што му је дата шаховска позиција и дистрибуција потеза Stockfish-a на дубини 10, на 10 милиона позиција. Minimax алгоритам функционише тако што један играч покушава да минимизује вредност евалуације за дату позицију, а други да га максимизује. Симулацијом игре на одређену дубину може се утврдити скоро оптималан потез. Алфа-бета орезивање је дорада овог приступа која динамички одбацује одређена подстабла стабла свих могућих потеза и њихових евалуација у односу на остале потезе који су до тад прегледани.

Приликом имплементације овог приступа јавила су се два проблема. Први проблем, у завршницама у којима остаје мало фигура модел није могао да види секвенце које воде ка победи другог играча, овај проблем је решен додавањем адаптивне дубине која зависи од броја фигура које су остале на табли. Други проблем, време које је моделу потребно да евалуира позицију је дуго за минимакс алгоритам будући да број могућих позиција расте експоненцијално са дубином исто расте и време рачунања најбољег потеза. Овај проблем је делимично решен имплементацијом алфа-бета орезивања које орезује гране стабла могућих позиција ако је претходно утврћен бољи потез исте дубине.

2.3.5. NNUE (Ефикасно ажурирајућа неурална мрежа)

Поред неуобичајеног начина кодирања позиције, сама архитектура мреже⁶ је поприлично једноставна.

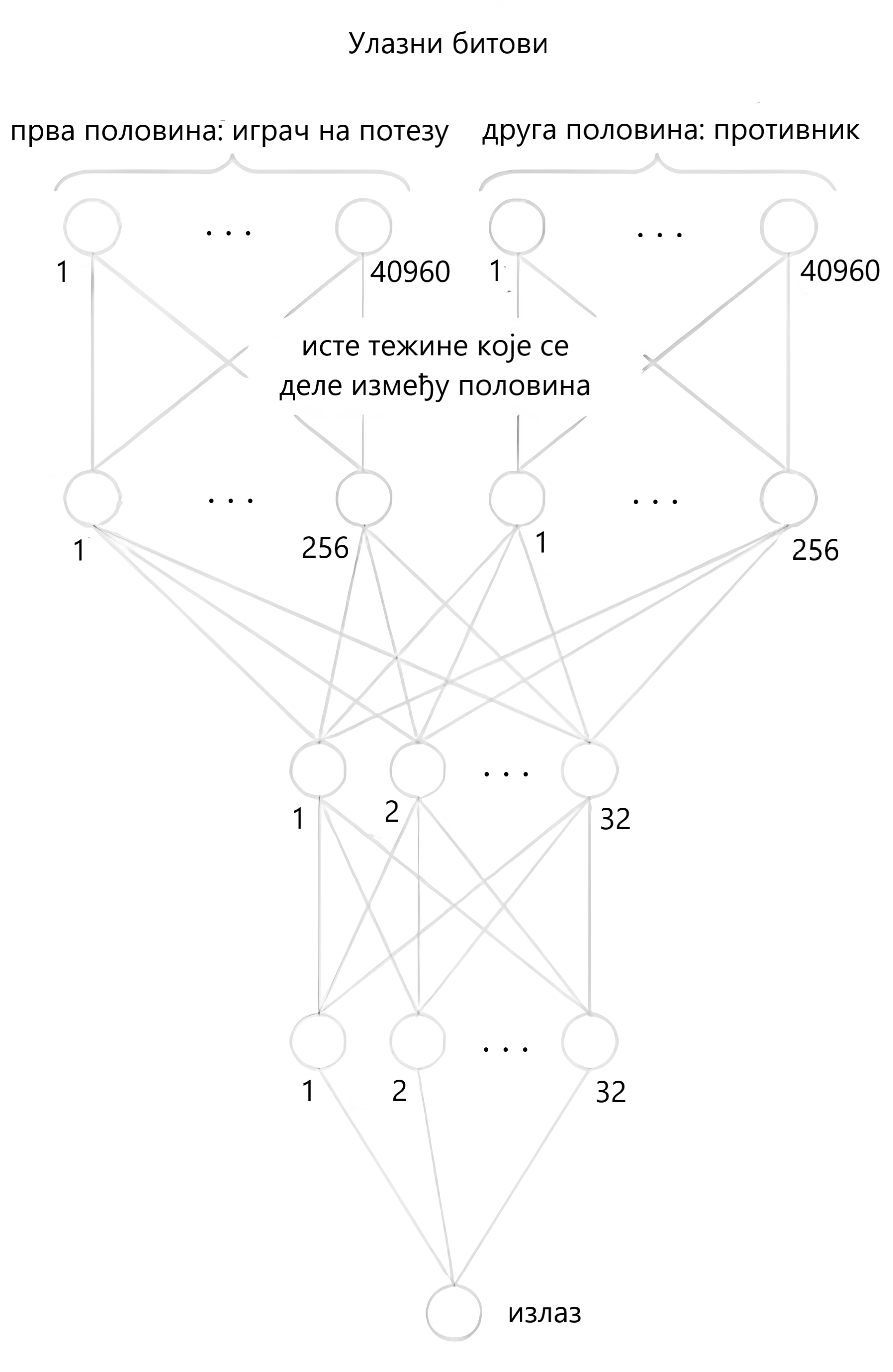
Постоје две половине, једна за страну која је на потезу, једна за противника. Свака од половина има за улаз кодирану позицију која је густо повезана са следећим слојем од 256 неурона. Корисно је то што је могуће користити идентичне тежине између ова два слоја у првој и другој половини. На пример, тежина која повезује бит „свој краљ на е1, пијун на а2” са првим чвором у следећем слоју, је иста као тежина која повезује бит „противнички краљ на е8, противнички пијун на а7”. Притом, ако се користе 8-битне и 16-битне вредности за параметре неуралне мреже, ово својство нам омогућује ефикасније рачунање помоћу напредних CPU инструкција.
Након првог слоја, две половине се спајају у густо повезани слој од 32 неурона, који је потом густо повезан са још једним слојем од 32. Последњи слој се састоји од једног неурона и представља евалуацију позиције.
Kоришћенa је ClippedReLU активациона функција између свака два повезана слоја. Вредности мање или једнаке нули сликају се у нулу, вредности између 0 и 1 се сликају саме у себе, а вредности веће или једнаке од 1 се сликају у 1.
За одређивање потеза, коришћен је minimax алгоритам, где бели играч покушава да максимизује, а црни играч да минимизује евалуацију.

3. Тренирање

Све мреже, осим MCTS методе, су трениране на скупу података од око 6,7 милиона шаховских позиција. Свака архитектура показује стабилну конвергенцију.

Метода која користи Монте Карло претрагу стабла се показала као сувише рачунарски захтевна, и због тог разлога није било могуће адекватно тренирати ту мрежу.

Модел	ResNet	„Две главе”	Ексклузивно евалуциони	NNUE
Batch size	$512$	$512$	$512$	$2048$
Стопа учења	$10^{-3}$	$10^{-3}$	$10^{-3}$	$10^{-3}$
Стопа смањења стопе учења	$/$	$/$	$10^{-4}$	$10^{-4}$
Број епоха	$20$	$20$	$15$	$50$
Оптимизатор	Adam	Adam	Adam	AdamW
Функција грешке	CrossEntropyLoss	За полису: CrossEntropyLoss, за евалуацију: MSE. Сабирају се и пропагирају уназад.	MSE	MSE
Scheduler	max, patience $= 2$	max, factor $= 0.5$, patience $= 2$	$/$	min, factor $= 0.5$, patience $= 5$

4. Резултати

Главна метрика која мери успешност одређеног модела или играча у шаху јесте његов ЕЛО¹¹ рејтинг. Будући да одређивање ЕЛО рејтинга захтева играње великог броја партија са моделом чији се ЕЛО рејтинг већ познаје, а то изискује велику количину времена одлучено је да се успешност модела мери статистичком методом Кендалов тау.

4.1. Кендалов тау

Кендалов тау¹² или Кендалов коефицијент корелације рангирања јесте статистичка мера која одређује корелацију две опсервације једне појаве. У случају овог рада Кендалов тау мери однос евалуације задате позиције наведених модела и модела Stockfish на дубини претраге 10 чији се резултат сматра истинском вредношћу. Екстремне вредности Кендаловог тау су -1 и 1, где вредност од -1 означава негативну корелацију (конкретно, један модел би одредио евалуацију као +х, а други као -х), вредност 0 означава одсуство било какве корелације док вредност 1 означава позитивну корелацију.

4.2. Графици

Следећи графици приказују корелације између евалуације позиције сваког од модела, сем MCTS методе, и евалуације коју је израчунао најбољи шаховски рачунар Stockfish на дубини претраге 10. Будући да је одговор РесНет модела потез, а не евалуација задате позиције, она се мерила моделом Stockfish из новонастале позиције ради рачунања корелације.

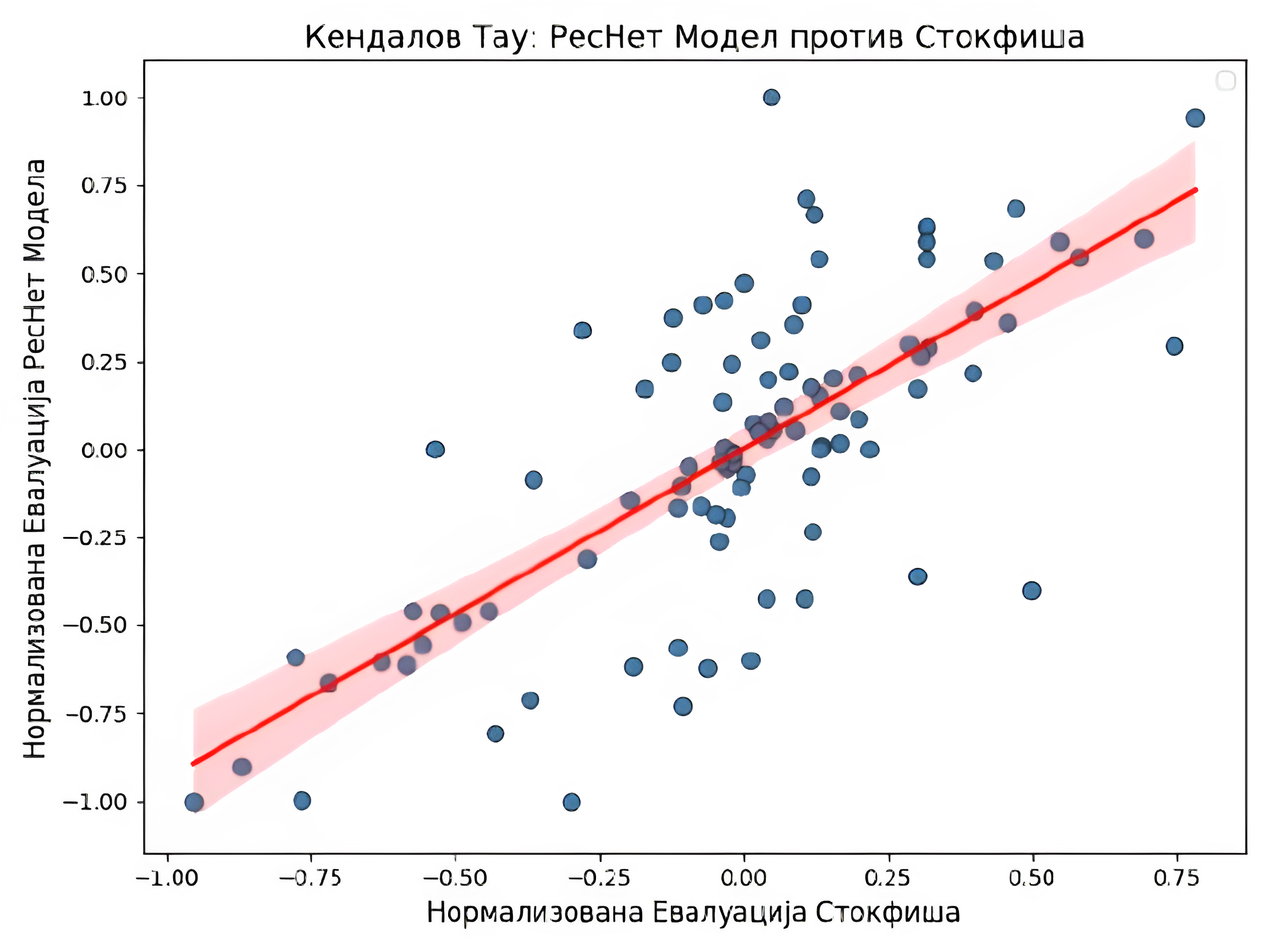
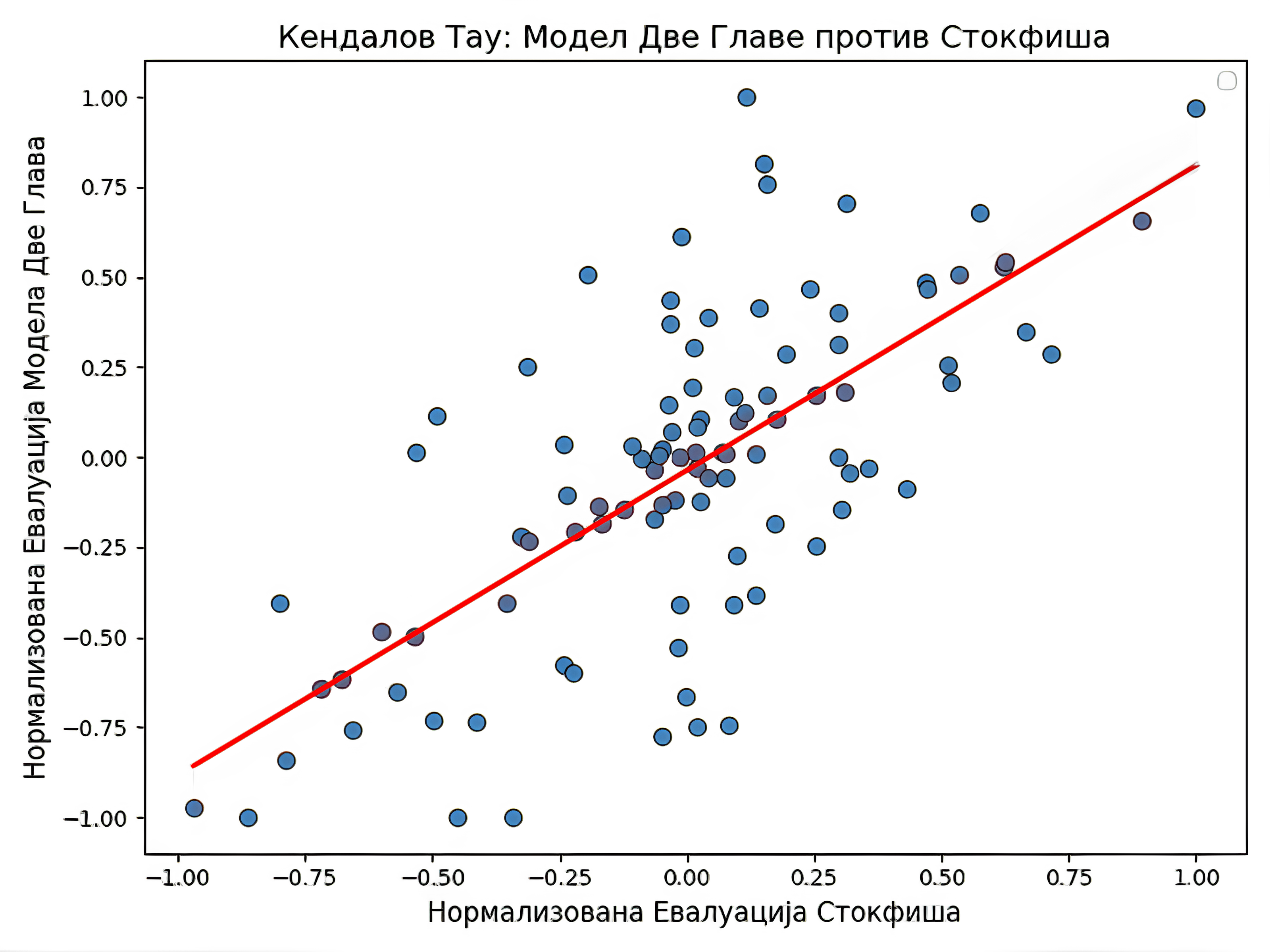
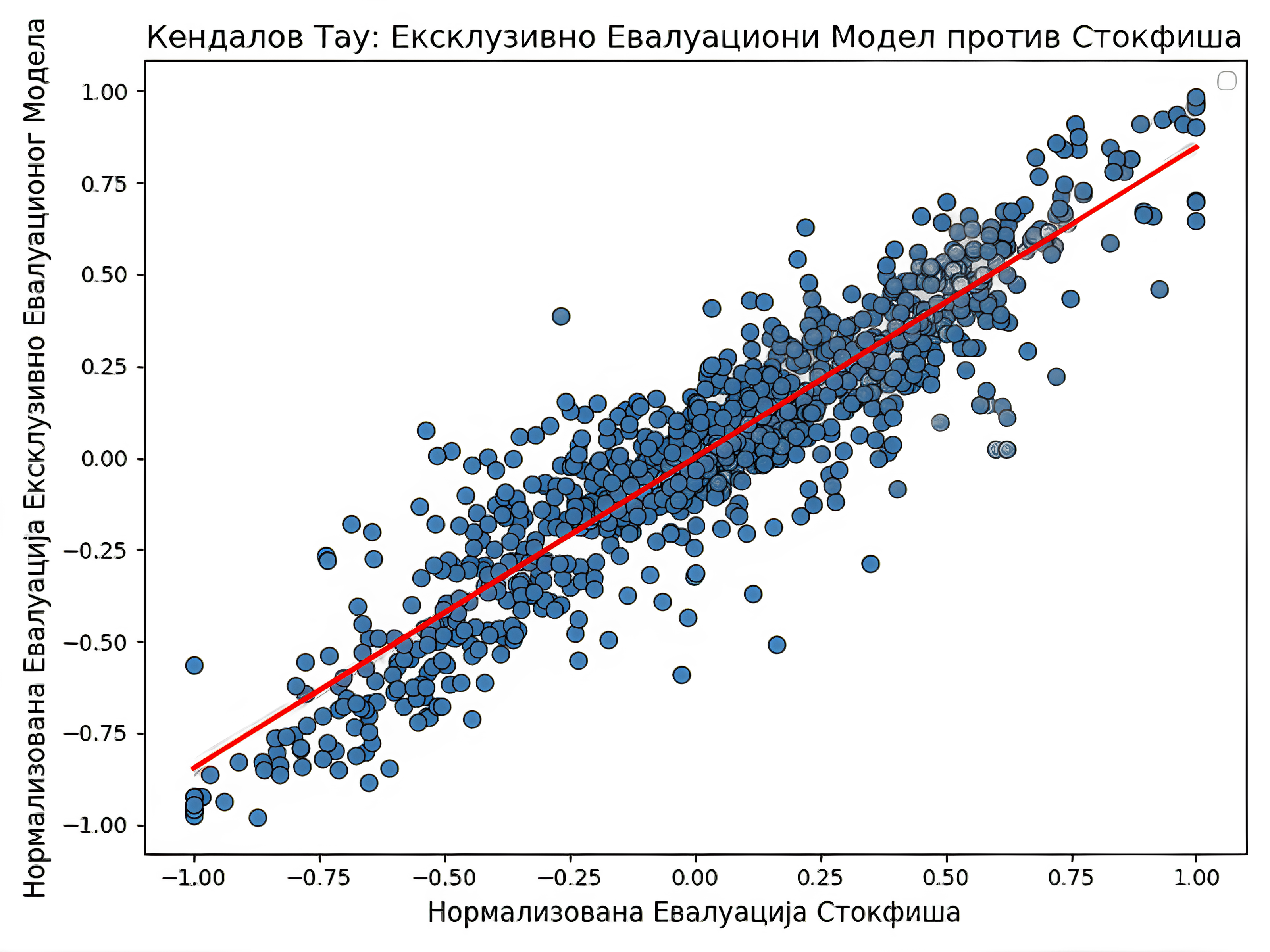
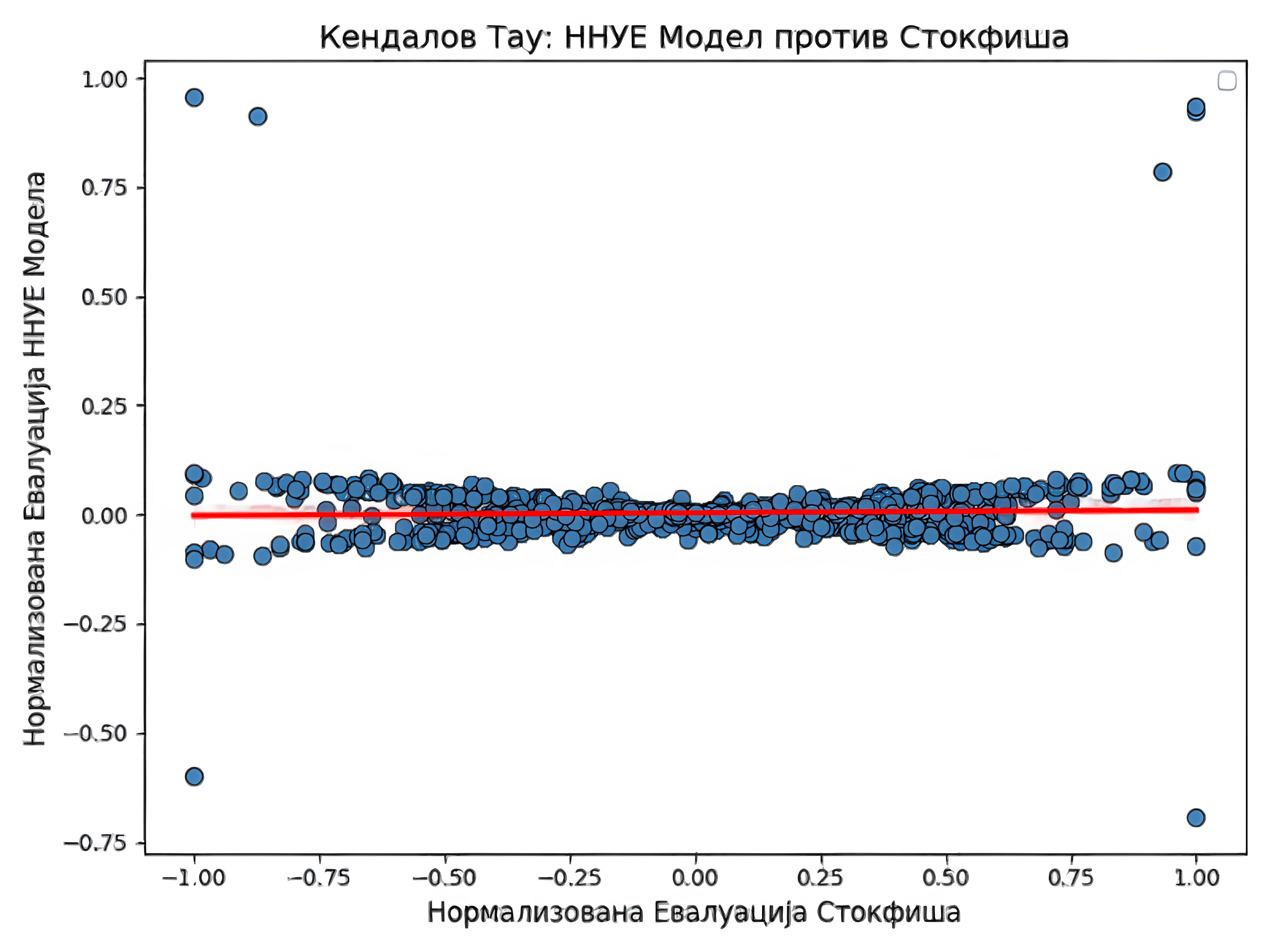
Модел	ResNet модел	Модел „Две главе”	Модел екс. евалуације	NNUE
Кендалов тау	$0.508138735333366$	$0.4762867857297649$	$0.7435471096073809$	$0.027304966680253697$

4.3. Дискусија

Прва два модела у табели имају поприлично сличне резултате, што се може објаснити релативном сличношћу у самој архитектури. Примећује се знатан скок у перформансама модела ексклузивне евалуације. То може да има пар узрока. Први је једноставан. Фокусирање мреже само на евалуацију позиције јој омогућује да се боље оптимизује за ту сврху. Други разлози се тичу саме архитектуре, попут веће дубине и повећавање броја филтера на крају у односу на почетак мреже. Нажалост, такође се примећује комплетан неуспех код мреже заснованој на NNUE архитектури. То сугерише на то да је за тај број параметара једноставно неопходно много више висококвалитетних података. Тај поглед потврђује чињеница да је Stockfish додатно трениран на генерисаним партијама другог по реду шаховског рачунара LeelaChessZero, који је заснован на архитектури рачунара AlphaZero. Такође, могуће је да је дошло до грешке приликом дељења параметара између две половине мреже.

5. Закључак

Пројекат се бавио развојем и имплементацијом 5 различитих модела који су имали за циљ да науче да играју шах по угледу на најбољег шаховског рачунара садашњице. Модел екслузивне евалуације, чија тренирана евалуациона функција која одређује који је играч у предности, упарен са minimax алгоритмом зарад проналажења најбољег потеза, је показао најбоље резултате. То сугерише је да могуће, са релативно мало рачунарске моћи, развити обећавајући шаховски рачунар који је способан да победи просечног играча шаха.

6. Даљи рад

Узимајући у обзир само колико различитих позиција могу да се јаве у једној партији шаха, очигледно је да је за бољи шаховски рачунар неопходно јако велики број висококвалитетних података, а за обраду свих података је потребно пуно компјутерске моћи.

У случају да није могуће набавити још рачунарске снаге, резултати најбољег модела у овом раду ипак показују да је можда довољно имати дубоку мрежу и добар minimax алгоритам. Испитивање те хипотезе би био централни фокус у даљем раду на овом пројекту.

Једна од могућности за оптимизацију minimax алгоритма јесте коришћење принципа динамичког програмирања за памћење евалуација позиција како би се избегла поновна обрада једних те истих позиција. Ова оптимизација би могла да смањи време извршавања и до двадесет пута и повећа дубину претраге чиме би се шаховска вештина програма знатно повећала.

Такође, отварање у шаху је једно од најбитнијих фаза сваке партије, међутим постоји могућност да је у бази података оно недовољно заступљено. Креирање обимне књиге отварања може знатно утицати на перформансе рачунара у реалним партијама.

7. Референце